Introduction
Blood pressure has been shown to be a strong indicator of cardiovascular health, particularly the coronary outcome. Increased systolic blood pressure (SBP) reflects changes in the arterial wall stiffness and vascular structure, whereas elevated pulse pressure (PP) predicts parallels between aortic atherosclerosis and the stiffening of conduit vessels [1]. Notwithstanding, the role of central pressure in clinical outcomes is increasingly recognized and central pressure seems to be more relevant to cardiovascular events than peripheral pressure [2]. Although invasive pressure waveform recordings are often considered the gold standard for central blood pressure (BP) measurements, invasive examinations have only been performed in a limited number of studies and not as part of daily clinical measurements [3]. Therefore, the pressure waveforms of the central arteries must be extracted from an analysis of surrogate waveforms for noninvasive pressure measurements. These waveforms are usually acquired using applanation tonometry of other easily available sites, particularly the radial artery, to which an arterial transfer function is applied [4,5]. Since the use of a universal transfer function (algorithm approved by Food and Drug Administration) is limited to the upper limbs, only the carotid artery and ascending aorta PP can be assessed via this technique [6].
Applanation tonometry is a well-known method to noninvasively record both central and peripheral pressure waveforms, which are then subjected to calibration or mathematical calculation. It is worth noting that the assessment of arterial pressure waveforms using applanation tonometry of the radial or carotid arteries can be technically and anatomically challenging and its measurement still lacks accuracy and has not found wide clinical application. This technique requires the operator to apply a hold-down mild pressure flattening the arterial wall to avoid the PP cushioning and obtain the optimal applanation, which occurs when the resulting waveform has a stable baseline [3,4]. Therefore, applanation tonometry has been reported to need a skilled investigator. Moreover, it requires specialized equipment and cannot be applied to all subjects and all arterial sites [7]. Furthermore, it assumes that the artery is compressible, which may not be true for carotid and conduit arteries [8].
However, other modern techniques and methods including echo tracking [9] and tissue Doppler imaging (TDI) [10] have made it possible to assess the central pressure waveform noninvasively. Today, high-resolution B-mode ultrasonic imaging of the carotid artery is familiar, feasible, and widely used in the diagnosis of atherosclerosis in imaging laboratories as it provides quantitative information of the intima-media thickness and lumen diameter and an assessment of the degree of stenosis as well as of plaque morphology [11]. Moreover, numerous studies have confirmed that temporal sequences of B-mode ultrasonic images analyzed with appropriate image processing techniques, may be used for extracting an arterial distention waveform as well as the arterial wall texture and elasticity features [12-14].
If arterial distention curves obtained using echo tracking methods are calibrated appropriately and accurately, the local PP achieved might be applied to more arterial sites and various subjects [15,16].
Because distension waves can be obtained in subjects and at arterial sites where applanation tonometry and the transfer function are not reliable, or not possible for technical reasons, the assessment of the BP waveform via an ultrasonic examination of arteries in combination with an appropriate automatic image processing technique might provide a more practical alternative to applanation tonometry. The objective of the present study is to introduce and implement a novel noninvasive ultrasonic method to derive the pressure waveform of the carotid artery. The proposed technique is based on a theoretical equation relating the PP to the blood flow velocity and arterial wall distention, both of which can be obtained by processing consecutive sonograms. The resulting pressures are calibrated using the mean and diastolic BPs of the radial artery.
Materials and Methods
Description of the Pressure Waveform Equation
The association of a pressure change with the rapid velocity change across a pressure wave in pipe systems is well known. The basic physics of linear momentum yields the fundamental equation of a water hammer (Joukowsky’s equation), to which accordingly, pressure and velocity changes are related as follows [17]:
where ρ denotes the fluid density, pwv represents the water hammer wave speed (pulse wave velocity), and Δp and Δv indicate the pressure and velocity changes relative to the corresponding initial values, respectively. Furthermore, the water hammer wave speed in an incompressible fluid within a flexible pipe is as follows:
where ΔA denotes the cross-sectional area (CSA) changes relative to the initial CSA.
In Eq (3), we assumed that irrespective of the velocity distribution throughout the CSA, all CSA elements undergo the same relative increase. Furthermore, the consideration that the fluid is frictionless [8] in a large vessel system is acceptable.
Ultrasonic duplex imaging provides arterial blood velocity changes during the cardiac cycle [20], while the arterial CSA can be achieved from sequences of B-mode ultrasonic images [21]. The uniqueness of the proposed method is to consider Eq (3) during cardiac cycles. By extracting the involved variables from ultrasonic image sequences of the carotid artery, PP (Δp) might be achieved over the cardiac cycles.
To examine the clinical use of the proposed approach, consecutive sonograms of 20 subjects were analyzed using the following procedure.
Subjects
Participants in this study were 20 men (aged 36±9 years) with no history of cardiovascular disease, hypertension, smoking, or diabetes. Participants were selected according to the clinical conditions presented [22]. All participants provided written informed consent for the examination, and the ethics committee of Tarbiat Modares University approved the procedure of this study.
Data Acquisition
After 10 minutes of recumbent resting in the supine position, the right common carotid artery of the subjects, 2 cm below the bifurcation of carotid artery, was scanned longitudinally with a Sonoline Antares digital ultrasound scanner (Siemens, Erlangen, Germany) equipped with a 5-13-MHz linear transducer with harmonic capability. The transducer was placed at the lateral side of the neck where the maximum lumen diameter appeared and the typical double lines of the artery could be seen. The Audio Video Interleave (AVI) format of an image sequence of the common carotid artery with a frame rate of 30 Hz was transferred to a PC for postprocessing. Each recording contained three cardiac cycles. A custom analysis program written in the MATLAB environment (Math Works, Natick, MA, USA) was used for extracting consecutive images in the Bitmap (BMP) format from AVI movies. The internal diameter was estimated offline by using the maximum gradient algorithm, designed in Ultrasound Laboratory of Tarbiat Modares University by MATLAB software. The mentioned algorithm allows a quantitative evaluation of the diameter changes by processing consecutive ultrasonic images. This algorithm was described in detail and validated elsewhere [23].
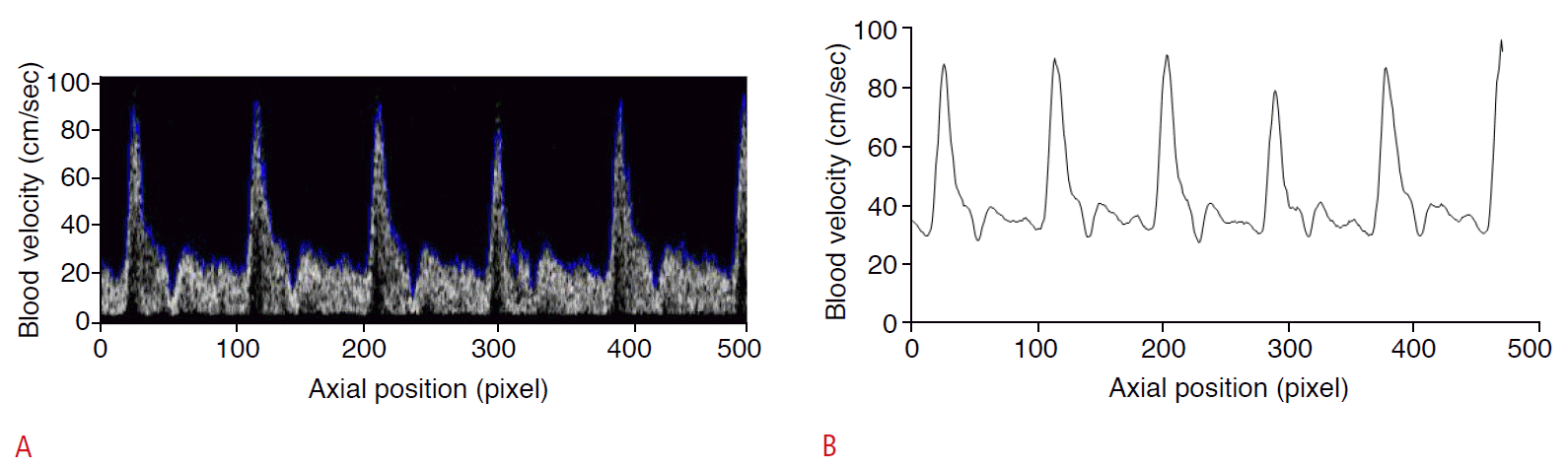
All images were processed by a custom MATAB program, in which the speckle noise was removed by setting an appropriate threshold for the grayscale level histogram [18,24]. Then, the envelope of the velocity profile was distinguished by the pixels after which the level value of at least 10 pixels was nonzero.
To extract the waveform of blood flow velocity, Doppler sonograms of the carotid arteries containing three cardiac cycles, from the same position expressed above, were recorded for all subjects. Recordings were made in the center of the artery, and the angle between the Doppler beam and the vessel orientation was chosen to be 60° to measure the correct Doppler shifts [25]. All images were processed by a custom MATAB program, in which the speckle noise was removed according to the method described [24]. In brief, several small areas outside the Doppler spectrum were selected and their grayscale levels were evaluated. The lowest grayscale level was set as the threshold for the grayscale level histogram. Then, the envelope of the velocity profile was distinguished by the pixels after which the level value of at least 10 successive pixels was nonzero. This avoids the possibility of considering noise speckles to be a velocity profile component.
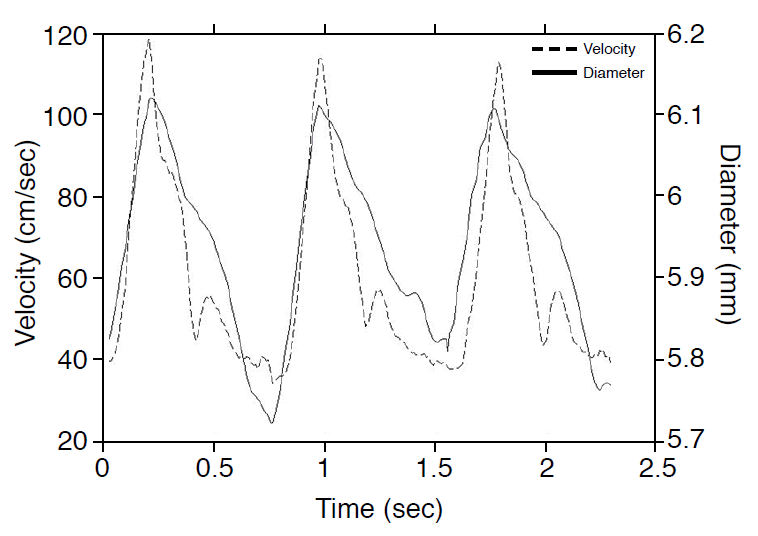
The internal diameter and blood flow velocity waveforms were recorded at different sample rates. Therefore, the recorded waveforms were decomposed into two parts: beginning to peak systolic and peak systolic to end diastolic. Then, the first portions of the waveforms were resampled at the sample rate of the maximum sample number existing in the first parts of the two waveforms. The second parts of the waveforms were resampled similarly. This ensures that the cardiac phases of the two waveforms are synchronized.
Arterial CSA was considered to be a circle and was calculated from the internal diameter. Arterial CSA, blood flow velocity, and CSA changes (instant waveforms minus the corresponding end diastolic values) during three cardiac cycles were substituted in Eq (3), and the PP waveform of the carotid artery was obtained during three cardiac cycles in all the subjects. The blood density was considered to be 1,060 kg/m3 [26]. Because the diastolic blood pressure (DBP) is assumed to be constant throughout the large conduit arteries [3], the DBPs measured from the radial artery of the subjects by using a calibrated digital sphygmomanometer were added to the achieved PP waves in order to obtain the BP wave. The sphygmomanometer calibration was carried out using an SES (SES-04 pump, Wild Heerbrugg, Heerbrugg, Switzerland) pump with the precision of 0.1 mm Hg at three pressure values: 100, 200, and 280 mm Hg. The mean error of the digital sphygmomanometer for the three pressure values was 0.7%. More details of the calibration are provided elsewhere [27].
The resulting waveforms were calibrated to the noninvasively measured mean radial artery pressure by using the following procedure in order to explore the potential of the proposed method to represent the noninvasively measured carotid pressure waveform.
Calibration Method
In general, pressure waveforms are calibrated by using the mean blood pressure (MBP) and DBP, assuming that they remain nearly constant throughout the arterial tree [3]. At the same time, the existence of a difference in the SBPs and PPs of the central and peripheral arteries should also be considered [28,29].
In this study, the MBP of the subjects was estimated using the SBP and DBP measured from the radial arteries of the subjects by using a calibrated digital sphygmomanometer. In other words, the MBP was assumed to be a summation of the DBP and one-third of the PP [21].
To estimate the MBPs of the carotid arteries from the pressure curves obtained from image processing, the numeric integral of the processed curves was calculated. Then, we considered a linear correlation between the MBPs calculated from the radial artery and image processing. That is, Pearson’s linear correlation between the MBP values resulting from two different methods could be written as follows:
where m and b denote the correlation line slope and the intercept of the correlation equation, respectively, and the subscripts rad and pro indicate the radial artery and image processing, respectively.
Moreover, according to the findings, the PP amplification between the central and the radial arteries is approximately 10-15 mm Hg in either normotensive or hypertensive subjects [8,27,28]. Furthermore, an invasive measurement has shown that the radial systolic pressure is 12±1 mm Hg higher than the central BP [30].
In this study, a mean value of 12 mm Hg for the amplification between the PPs of the carotid and the radial arteries (pprad= ppact+12) was considered. The calibrated factor (k) was defined as a fraction of the actual and the processed PPs of the carotid artery
( k = P P a c t P P p r o ) .
Therefore, two equations of the MBP correlation relation (Eq 4) and the PP amplification were substituted in the calibration factor definition to extract the subject-specific calibration factor.
Thus, assigning the same MBP and DBP to the arterial system and the pressure waveform at the carotid artery could be calibrated noninvasively over the cardiac cycle by multiplying the PP waveform of each subject with his own calibration factor. Note that the resulting calibration factor is only applied to the PP and the DBP is assumed to be the same in the radial and carotid arteries.
Statistical Analysis
The difference between the carotid PPs obtained from the radial artery PP minus the radial/carotid amplification and that obtained using the calibrated image processing method is expressed as the mean±standard deviation (SD). To evaluate the relationship between the corresponding PPs resulting from the previously described methods, we performed a Bland-Altman analysis [31] with 95% limited of agreements. All the statistical analyses were performed by SPSS ver. 16.0 (SPSS Inc., Chicago, IL, USA) and Microsoft Excel 2007 (Microsoft Corporation) environment.
Results
The profile of the blood flow velocity is extracted from the envelope of a Doppler ultrasound image (Fig. 1) and then, synchronized with the internal diameter waveform (Fig. 2).
Considering the CSA of the artery to be a circle makes it possible to calculate the CSA during three cardiac cycles. After substituting the CSA, instantaneous blood velocity, and CSA changes relative to the diastolic values in Eq (3), the PP waveform of the common carotid artery was extracted during three cardiac cycles for all the subjects.
To employ the previously described noninvasive calibration method, Pearson’s linear correlation between MBPs of the waveforms obtained by image processing and those measured on the basis of radial artery pressures was calculated. The correlation between the MBPs of image processing-based pressure curves and those measured from radial artery pressures is depicted in Fig. 3. According to the resultant linear correlation equation, the m and b values used for the calibration factor calculation were 1.011 and 9.799, respectively (Fig. 3).
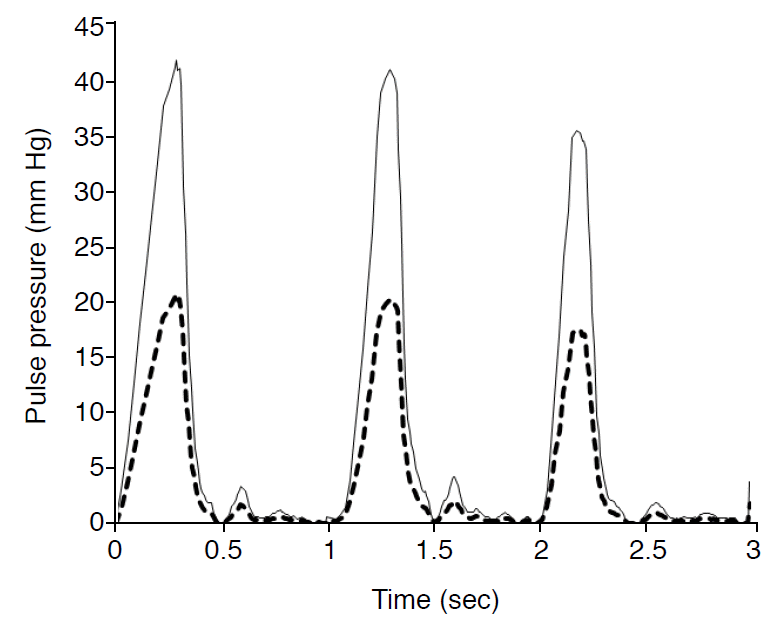
To achieve the calibrated PP wave, the calibration factor of each subject was multiplied with his own uncalibrated PP waveform of the common carotid artery obtained from sonograms (Fig. 4).
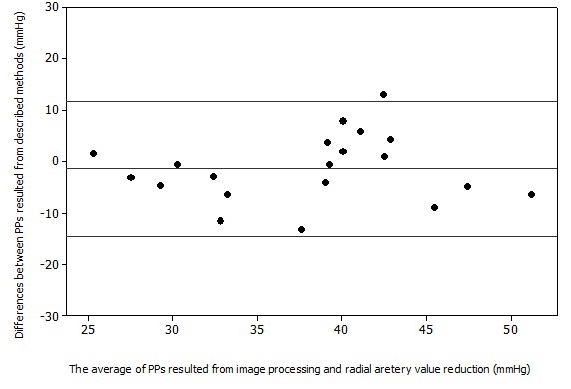
To assess the agreement between the calibrated PPs and the corresponding values measured via a standard sphygmomanometer, a scatterplot of the Bland-Altman analysis was drawn and the differences between the PPs measured by the abovementioned methods were plotted against the average values of the differently achieved PPs (Fig. 5). According to the scatterplot, the PPs obtained from image processing and those calibrated using the calibration factor have a good coherence with the PPs measured using a standard sphygmomanometer at the radial artery.
The mean absolute difference of the calibrated PPs and the clinically measured PPs was -1.333±6.548 mm Hg, and the mean value of the calibration factors was 2.224±0.721. The resulting differences fell within the Association for the Advancement of Medical Instrumentation (AAMI) recommended limits of acceptance between the standard and the automated methods of pressure measurement [32].
Discussion
Accurate computerized delineation of a pressure wave seems to be a novel idea for daily cardiovascular health monitoring [33,34].
Today, ultrasonic inspection is widely accepted as a noninvasive technique for general clinical applications. The ultrasound imaging feasibility of most vascular sites, cost effectiveness and its incorporation into cardiovascular imaging examinations without any additional equipment [10] encourage the idea of using the same imaging test to obtain an arterial pressure waveform, which might promote anatomical and functional information about arterial health. In this study, we established a novel ultrasonic method for pressure waveform achievement. Thus far, the results of the attempts related to the development of noninvasive ultrasonic techniques for pressure wave measurement have been notable.
Olesen et al. [35] applied an ultrasonic method for estimating 2D hemodynamic pressure gradients in a flow model, which mimicked the carotid bifurcation having 70% occlusion at the beginning of the internal carotid artery. Pressure gradients were calculated using Navier-Stokes equations in which the vector velocity fields were obtained by processing ultrasound radiofrequency data. The results were compared to the pressure resultant from 3D finite element modeling of a phantom. In the mentioned study, steady flow conditions were set up and the gravitational force and the out-of-plane velocity component were neglected [35].
Haluska et al. [10] acquired the pressure wave of the carotid artery from TDI and compared it with the tonometry results. They showed that there is a high correlation between the results of TDI-based pressure waveforms and those of tonometry with a difference of 5.36±5.5 mm Hg in systolic pressure values [10].
Moreover, studies in which the BP waveforms were assessed from echo tracking distension waves calibrated linearly or exponentially, reported that there is an underestimation of at least 2.5 ± 5 mm Hg in the carotid artery PP [15].
Consistently, the MBP derived from our novel method correlated well with the radial artery MBP (R=0.91) and the mean absolute difference of the calibrated PPs and the clinically measured PPs was -1.333±6.548 mm Hg, which seems to fall within the reported error regions.
All noninvasively acquired arterial pressure waveforms require calibration to a known BP, which may impose a potential source of measurement errors, particularly when inaccurate pressures are used for noninvasive calibration. However, noninvasive calibration is widely used in the literature and a literature review showed that central PP errors vary in the range of -32.5 to 8.1 mm Hg when noninvasive calibration to peripheral BP is applied [3]. Furthermore, Agnoletti et al. [36] showed that pressure waves of different arteries obtained as a result of applanation tonometry, which were calibrated using four different noninvasive methods, lead to a difference of 14-18 mm Hg in PPs.
Hope et al. [37] measured the noninvasive radial pressure waveforms and compared the impact of invasive and noninvasive calibration methods on the same central pressure waveform derived from a transfer function. They showed that noninvasive calibration resulted in an underestimation of 7±12 mm Hg in the estimation of the central systolic pressure. They found a significant difference between the radial waveform calibrated invasively and noninvasively and suggested that the differences were due to the invasive and noninvasive diastolic pressure of the aorta [37].
Van Bortel et al. [9] reported that noninvasively calibrated arterial distension waves caused by echo tracking are 3.4±6.9 mm Hg lower than the PP waves obtained from invasively calibrated tonometry. However, the differences between invasively and noninvasively derived and calibrated pressure waveforms are inevitable. Any difference between our image processing-derived pressure waveforms and the invasively derived ones may be attributed to the assumption that both the mean and the diastolic pressures remain unchanged throughout the arterial tree. However, the notion of exactly the same mean and diastolic pressure values from the central to the peripheral artery holds true only in invasive measurements of the central and peripheral BP [3].
Further, although a mathematical manipulation of the radial artery pressure waveform predicts the peak and through pressure well, the exact shape achievement requires an invasive measurement. Moreover, errors caused by the mathematical modeling between the peripheral and the central pressure waveform might be challenging [3,6]. Furthermore, the transfer function method is sensitive to noninvasive calibration errors and the accuracy of the results is affected by the calibration errors [36].
For technical reasons, applanation tonometry and the transfer function are not reliable, or not possible at all arterial sites, and the method proposed in this study, assessing the BP waveform via an ultrasonic examination of the arteries by using an appropriate automatic image processing technique, can provide a more practical alternative to applanation tonometry.
The proposed method as a noninvasive BP measurement technique suffers from the same limitation of calibration errors. In the present study, invasively measured BPs were not available and this may pose errors. Further, the error of the acquired pressures in our study may be associated partly with the incorrect estimation of the centerline velocity profile caused by the insonation angle error [24] and the weakness of the 33% rule as compared to the precise method of measuring MBP via an intra-arterial catheter [35].
Beulen et al. [38] extracted the local pressure waveforms in a phantom set up. Their method was based on a particle image velocimetry technique applied to the high-frame-rate ultrasound radio frequency data. This way, they circumvented the Doppler flow velocity errors because their implemented method required no beam steering and the relation between the pulse wave velocity (PWV) and the local pressure was derived with the assumption of a linear elastic thin-walled vessel. In their study, PWV was extracted by a flow-area (Q-A) method, which is restricted to the reflection-free periods of the cardiac cycle. It was shown that for carotid-like pulses, the reflection-free part of the Q-A loop was not clear and high-sample-rate techniques were required to obtain adequate sample points over the linear section of the loop [38].
A further potential limitation is the use of the mean value of 12 mm Hg for PP amplification. PP amplification has been reported to fall with aging [39]. Considering different values for younger and older subjects may improve the accuracy of the obtained pressure.
It is worth noting that according to AAMI recommendations, the acceptance upper limit between the difference of the standard and the automated methods for BP measurement is ±5 and ±8 mm Hg for mean and SD, respectively [31].
Another limitation from which the present study suffers is that this study consisted of only normal carotid arteries without pathological changes, such as the degree of carotid stenosis and the arterial CSA was assumed to be a circle, while this assumption has been a large trial in regions having irregular and asymmetric stenotic plaques. Nevertheless, in these regions, it might be required to record additional consecutive ultrasonic images from the transverse view of the artery, and then, arterial CSA can be outlined using segmentation methods. However, the same procedure can be used for the subjects who have hypo/hypertension; that is, once the correlation equation (slope, intercept) between the MBP values obtained from image processing and values measured from the radial artery was calculated for a group of subjects suffering from hypo/hypertension, Eq (5) is applicable to extract the patient-specific calibration factor for any typical patient having the same disease.
In the present study, the blood is assumed to be a perfect fluid. Therefore, the proposed method is expected to provide an appropriate inter-subject comparison of the pressure waveform shape and characteristics.
In spite of all the limitations, the error in the PPs obtained from our ultrasonic technique is similar to the reported results of other publications using different methods. It has been suggested that when a pressure wave is extracted from arterial wall displacement, no phase delay due to spatial separation or filter characteristics will affect the result [40]. Nonetheless, the methods in which the pressure curve is derived purely from a diameter wave neglect the effect of the blood flow and the viscoelastic properties of arteries on the pressure waveform and generally assign an exponential relationship between the diameter and the pressure [39]. However, theoretically, both the blood flow and wall properties determine the pressure waveform characteristics [18]. To the best of our knowledge, this is the first time that a pressure waveform is extracted practically from a theoretical equation considering both the blood flow and wall effects. This technique can be implemented for all arterial sites. Extraction of the other sites pressure waveform, particularly that of the radial artery, via the proposed technique in the present study and a comparison of the results with those of the carotid artery are suggested for future studies.
In conclusion, the results of this study suggest that arterial PP waveforms can be assessed using a noninvasive ultrasonic examination of arteries, promoting a noninvasive technique for clinical applications. We believe that the proposed method, having a high agreement with the literature, would overcome the drawback of simultaneously assessing pressure and diameter waves at specific sites for the estimation of the total arterial compliance and it would seem to overcome the reproducibility problems of common carotid artery tonometry with technical and anatomical causes.



 Print
Print facebook
facebook twitter
twitter Linkedin
Linkedin google+
google+

 Download Citation
Download Citation PDF Links
PDF Links PubReader
PubReader ePub Link
ePub Link Full text via DOI
Full text via DOI Full text via PMC
Full text via PMC




