AbstractPurposeThe purpose of this study was to compare the reliability of ultrasound-based shear wave elastography in regions of homogeneous versus heterogeneous elasticity by using two different probes.
MethodsUsing acoustic radiation force impulse (ARFI) elastography, we measured the shear wave velocity (SWV) in different lesions of an elastography phantom with the convex 4C1 probe and the linear 9L4 probe. The region of interest (ROI) was positioned in such a way that it was partly filled by one of the lesions (0%, 25%, 50%, 75%, and 100%) and partly by the background of the phantom (100%, 75%, 50%, 25%, and 0%, respectively).
ResultsThe success rate was 98.5%. The measured value and the reference value of SWV correlated significantly (r=0.89, P<0.001). Further, a comparison of the two probes revealed that there was no statistical difference in either the mean or the variance values. However, the deviation of SWV from the reference was higher in the case of the 9L4 probe than in the case of the 4C1 probe, both overall and in measurements in which the ROI contained structures of different elasticity (P=0.021 and P=0.002). Taking into account all data, for both probes, we found that there was a greater spread and deviation of the SWV from the reference value when the ROI was positioned in structures having different elastic properties (standard deviation, 0.02±0.01 m/sec vs. 0.04±0.04 m/sec; P=0.010; deviation from the reference value, 0.21±0.12 m/sec vs. 0.38±0.27 m/sec; P=0.050).
ConclusionQuantitative ARFI elastography was achievable in structures of different elasticity; however, the validity and the reliability of the SWV measurements decreased in comparison to those of the measurements performed in structures of homogeneous elasticity. Therefore, a convex probe is preferred for examining heterogeneous structures.
Ultrasound-based shear wave elastography is a novel method for quantifying tissue stiffness. Many organs have been examined by this new method, such as the abdominal organs [1-3], including transplanted organs [4,5], prostate [6], testis [7] cervix [8], muscles [9,10], vessels [11,12], thyroid [13], and salivary glands [14,15]. The purpose has mostly been to differentiate between benign and malignant focal lesions or to evaluate fibrotic changes. The possible applications of elastography seem to be unlimited although the clinically viability and feasibility of these applications for daily use remain to be proven. The first guidelines on the clinical use of ultrasound elastography have been published, giving recommendations on how to use this new technique, mainly limited to the liver and the breast [16-18]. Nevertheless, this new method is in an early state of clinical routine and many questions remain unanswered.
Shear wave elastography modalities were developed under common material assumptions such as tissue homogeneity (at least within a specific region) and other factors such as isotropy. However, their reliability and precision under different measurement conditions remain unknown [19]. The measurement of shear wave velocity (SWV) in inhomogeneous tissue and, often associated, in tissues having different elasticity properties is very common in everyday clinical practice, for instance, measurements in tumors or in the kidney, where both the renal cortex and the medulla are included because of the fixed size of the region of interest (ROI). The aim of this study was to compare the reliability of acoustic radiation force impulse (ARFI) elastography in regions of homogeneous versus heterogeneous elasticity and to evaluate whether there is a significant difference between the convex 4C1 probe and linear 9L4 probe measurements.
For our study, we used Virtual Touch tissue quantification (VTTQ; product version VB21) from Siemens (Erlangen, Germany), which applies the ARFI imaging technology. This technology was described in detail by Nightingale et al. [20], Lazebnik [21], and John and Liexiang [22]. In short, the investigator positions the ROI (fixed size of 6 mm×10 mm for the convex 4C1 probe and 6 mm×5 mm for the linear 9L4 probe) by using B-mode ultrasound for imaging-based localization. Upon the touch of a button, an acoustic push pulse is sent directly lateral to the ROI. As a result, the tissue experiences a small displacing mechanical force that leads to the propagation of shear waves (SWV) traveling perpendicular to the push pulse. The velocity of these SWV is detected by tracking beams and is displayed on the screen next to the measurement depth (Fig. 1). The SWV value characterizes the elasticity of the measured material: the higher the SWV measurement, the stiffer is the target material. When the symbol “XXXX” is shown, no valid measurement could be acquired. Further, the confidence level determined by the SWV estimation algorithm was below 0.8 on a 0 to 1 scale. This is because the individual velocity estimates between the tracking beams differed too much to provide a reliable value. This feature helps to ensure measurement quality, preventing a misinterpretation of invalid measurements [23].
We performed measurements on the “049 Elasticity QA Phantom” (Computerized Imaging Reference Systems [CIRS], Norfolk, VA, USA) with the linear 9L4 (7-MHz) probe and the convex 4C1 (4-MHz) probe. This phantom contains four spherical lesions (diameter, 20 mm; at a depth of 35 mm) of different, defined stiffness values (denoted by Young’s modulus E: 7.3 kPa, 18.8 kPa, 45.9 kPa, and 61.5 kPa), embedded in a homogenous mass of Zerdine (E=29.4 kPa).
Young’s modulus can be related to the SWV as follows [19].
According to the manufacturer of the phantom, the Poisson ratio can be estimated to be approximately 0.5 and the density to be about 1.0 g/cm³ [24]. By simplifying the above equation, we obtained the following.
By using the latter equation, we can convert the Young’s modulus value of the manufacturer’s data (denoted in kPa) into SWV (denoted in m/sec). Therefore, the SWV measured by VTTQ can be directly compared with the “true” stiffness values given by the manufacturer.
The phantom was positioned on a digital weighing scale (Soehnle Page Profi Küchenwaage, Leifheit AG, Nassau an der Lahn, Germany) placed on a wooden board (as a stable base). The scale enabled the pressure exerted by the probe to be monitored and controlled with the aim of keeping it as low and as constant as possible. To reduce operator dependence, the measurements were performed with the probe held in position by a supporting arm (Fig. 2A, B). The arm was adjustable in height and length; therefore, the measurement on each lesion could be performed as follows: the ROI was positioned in such a way that it was partly filled by one of the lesions (0%, 25%, 50%, 75%, and 100%) and partly by the background of the phantom (100%, 75%, 50%, 25%, and 0%, respectively); an example is shown in Fig. 3. To achieve the coverage of 25%, 50%, and 75% as precisely as possible, a scale was used for measuring (on the screen) the distance from the upper border of the ROI to the upper border of the lesion. Accordingly, the reference values were calculated from the manufacturer’s data on a percentage basis. For example, the reference value for the condition “ROI 25% in lesion 1” was calculated as follows: 0.25×7.3 kPa (elasticity of the softest lesion)+0.75×29.4 kPa (elasticity of the background)=23.875 kPa (2.82 m/sec). When measuring 100% in the lesion, the ROI was placed in the middle of the lesion. In order to measure 100% in the background, the ROI was placed closely above the lesion. The ROI was always positioned on the midline, perpendicular to the phantom surface. Because of the positioning of the ROI as described above, the variance of the measurement depth was approximately 2.0 cm in the case of the convex 4C1 probe and 1.0 cm in the case of the linear 9L4 probe. Ten valid measurements were performed per measurement setting (measuring four different lesions by placing the ROI in five different ways by using two different probes). The setup was only touched when moving on to the next lesion or when changing the probe. If a measurement was not valid, “XXXX” was displayed. The number of invalid measurements was noted, and the measurement was repeated until a valid value was obtained.
For the statistical analysis, IBM SPSS Statistics ver. 20 and 22 for Windows (Armonk, NY, USA) were used. As is generally recommended for the ARFI method, we used the average of ten single measurements for our analysis (i.e., the mean of ten values per measurement site). Hence, the resultant sample size (as displayed in the tables) represents one tenth of all individual measurements performed.
The success rate was calculated by the quotient of the number of valid measurements divided by the total number of measurements performed. The correlation of a measured value and the reference value was quantified by Pearson´s correlation coefficient and illustrated as a scatter plot. To clarify the distribution of the values, a quadratic interpolant was drawn through the scatter plot of the measurement points and a bisecting line was added. A linear regression analysis was employed to evaluate the relationship between the probe and the deviation of the measurement values from the reference values. As a result, the regression coefficient (B), the 95% confidence interval, and the two-sided P-value were used.
Moreover, the data were divided into two groups: one of them included the measurement series in which the ROI was completely positioned in one structure (0% and 100% in the spherical lesion), and the other group involved the series where the ROI contained partly the lesion and partly the background material of the phantom (25%, 50%, and 75% in the spherical lesion). With the unpaired t test, the two groups were compared. Further, the same test was used for comparing the 4C1 and the 9L4 probes within the single fractions. The parameters for the comparison were the absolute measured value, the standard deviation, and the divergence of the SWV from the reference value. This divergence was defined as the absolute value of the difference between the reference value and the average SWV of ten measurements (Abs_D). A two-sided P-value of <0.05 was considered significant.
The mean values of the SWV and their divergence from the reference value for each probe, averaged over all lesions, are displayed in Table 1 (group 1, in total). The success rate was 98.5% (number of invalid measurements, 6). The correlation between the measured SWV and the reference value was high (r=0.89, P<0.001). The scatter plot in Fig. 4 illustrates this relation for each probe. The scatter points of the convex probe were grouped closer to the reference line (non-continuous line), whereas the points of the linear probe were generally located deeper below the reference line.
The interpolation shows that even the convex probe tended to underestimate the stiffness if the SWV was higher than 4.0 m/sec. Moreover, the interpolants of the two probes are not equal; that is, different probes showed different results. The linear regression analysis showed that the choice of the probe had a significant influence on the divergence of the measured values from the reference values (regression coefficient B, 0.17; 95% confidence interval, 0.03 to 0.31; P=0.021).
Further analysis with the unpaired t test was performed by differentiating the following three groups: group 1 concluded all measurements, group 2 involved only series in which the ROI was wholly positioned in one homogenous structure (100% in the lesion or 100% in the background of the phantom), and group 3 contained only the series in which the ROI was placed partly in a spherical lesion and partly in the background. Regarding the mean, values measured by the 9L4 probe were, when averaged across all lesions, not significantly smaller than those by the 4C1 probe (in accordance with Fig. 4). Concerning the standard deviation, there was no statistical difference. The divergence of SWV from the reference was higher in the case of the 9L4 probe than in the case of the 4C1 probe, both overall and in those measurements in which the ROI contained structures of different elastic properties. In group 2 (ROI involves only one structure), there was no significant difference between the two probes, but the tendency was that higher deviations were observed for the convex scanner (Table 1).
Moreover, we evaluated whether the discrepancy of the measured value from the reference value and the standard deviation were higher when the ROI involved structures having different elasticity. For this, an unpaired t test was used by subdividing the data in groups 2 and 3 (see above). Compared with measurements where the ROI was positioned in a homogenous structure (group 2), there was a significantly higher difference from the reference value as well as a significantly higher standard deviation in group 3 (Table 2); that is, the SWV spread more and deviated more from the reference when the ROI was positioned simultaneously in structures having different elastic properties.
The aim of our study was the evaluation of ARFI quantification on the borderline of different elasticity properties. Thus, we positioned the ROI in an elastography phantom in such a way that it was partly filled by one of the lesions (0%, 25%, 50%, 75%, and 100%) and partly by the background of the phantom (100%, 75%, 50%, 25%, and 0%, respectively).
There are a few limitations of this study, mainly associated with the properties of the phantom used. However, one has to consider that to the best of our knowledge, this is the only available phantom of this type and using it offered the chance to perform measurements in a completely standardized setting. The accuracy of the given percentages of how we placed the ROI was limited by the round shape of the lesions: as the width of the ROI is relatively small compared to the diameter of the lesion, the surface of the spherical lesion can be assumed to be approximately flat. Therefore, the influence on the calculated values should be quite small.
The further the ROI was positioned within the lesion, the greater was its depth because of the physical configuration of the phantom: as the depth is considered to be an influential factor on SWV, this might have impaired our results [24,25], but as the difference in depth was only 10-20 mm, the influence should not be too high. Nevertheless, these limits should be kept in mind when interpreting the following results and should be respected in further scientific investigations.
The success rate of 98.5% was high and comparable to another study on the phantom “CIRS 049 QA” in which the ROI was only placed in homogenous structures (0% and 100% intralesional) (success rate, 100%) [24]. Plotting the measured values and the reference values in a scatter plot (Fig. 4) revealed that the observations were dispersed relatively close to the reference given by the bisecting line. Therefore, the measurement of the SWV in heterogeneous structures seems to be principally feasible.
The linear scanner produced multiple underestimated values. The convex probe seemed to be closer to the reference values, which was confirmed in the quantitative analysis (deviation from the reference value for 4C1: 0.22±0.18 m/sec vs. for 9L4: 0.39±0.25 m/sec; P=0.021). A disparity of the measurements by the 4C1 and the 9L4 probes was also ascertained in other studies on the phantom and on the liver [24,26]. This could be attributed to the various properties of the probes: the geometry (convex vs. linear) with different elevations and footprints, the frequency of the push pulse to generate the shear waves (2.67 MHz vs. 4.00 MHz), and the frequency of the tracking beams to detect the shear waves (4 MHz vs. 7 MHz).
When subdividing the data dependent on the positioning of the ROI in homogeneous or heterogeneous areas (group 2, ROI 0% and 100%; group 3, ROI 25%, 50%, and 75% in a spherical lesion), interestingly, the convex probe was significantly more precise in group 3 only (Abs_D for 4C1: 0.22±0.21 m/sec vs. for 9L4: 0.54±0.22 m/sec; P=0.002). However, in the “homogeneous” group, the values measured by the linear probe were (not significantly) close to the reference value (Abs_D for 4C1: 0.24±0.14 m/sec vs. for 9L4: 0.18±0.09 m/sec; P=0.362). This was in accordance with the results from other studies of our working group (unpublished work) and with the results from the Yamanaka et al. [24] who carried out SWV measurements in the center of spherical lesions to evaluate the feasibility of the ARFI method in structures having known, homogenous elasticity.
In conclusion, heterogeneous structures and/or their boundaries seem to be a stronger confounding factor for the linear probe than for the convex probe. This might be partly caused by the different properties of the probes mentioned above. Considering that the linear probe uses higher frequencies, our observations seem surprising as the axial and lateral resolutions have a fundamental influence on the detection of SWV. Interestingly, this applies only to measurements in the case of homogeneous elasticity. Using ARFI, we detect SWV by “plane wave imaging,” and perhaps, the software for the detection of SWV in “plane wave imaging” is better adapted for the convex probe than for the linear probe. Finally, there are many possible technical and physical reasons for the differences observed between the probes. However, the effect that contributes to the observed differences cannot be explained by the experimental setting. Including the data from both probes, we found that the divergence from the reference value as well as the deviation of the SWV was significantly higher when the ROI included two structures having different elasticity properties than in measurements where the ROI was positioned in one structure of homogenous stiffness (Table 2). As mentioned previously, ARFI quantification and many other elastography methods were evolved under common material assumptions such as tissue homogeneity (at least within a specific region) and other factors such as isotropy.
Further, on the boundaries, shear waves are partly reflected and/or absorbed. Thus, a change in their direction as well as a change in their intensity and velocity is possible. Consequently, the accuracy of the SWV calculation deteriorates and this might result in artifacts and misinterpretation [19]. In our results, the absolute value of the deviation from the reference and of the dispersion have to be considered to be small (-0.17±0.06 m/sec and -0.02±0.01 m/sec). However, the SWV was measured under simplified conditions with the ideal maximum of one boundary. When performing measurements on organs, the push pulses, shear waves, and tracking beams push on multiple boundaries. Therefore, our observations might become more important depending on the heterogeneity of the measured tissues. To the best of our knowledge, comparable studies are missing.
Several papers on ultrasound-based elastography of the liver recommend that the ROI should not include any large vessels or biliary structures, probably to include as much parenchyma as possible, as this is the target of interest [27-29]. On the basis of the abovementioned results, we could, for the first time, confirm this recommendation with respect to the technical aspects. The possibility of using a B-mode image as an aid to position the ROI gains importance in this respect and presents a clear advantage of the ARFI method over transient elastography.
In conclusion, according to our data, quantitative ARFI elastography was feasible in structures with diverse elasticity properties. However, the validity and reliability decreased, compared to measurements in structures with homogenous elasticity. Hence, the ROI should be placed in homogeneous regions whenever possible, avoiding obviously heterogeneous structures such as large vessels or calcifications. Further, according to our results, the convex probe is the preferred probe for examining heterogeneous structures. Confirmation by further studies with a larger sample size and ideally in a clinical setting is necessary.
References1. Goertz RS, Amann K, Heide R, Bernatik T, Neurath MF, Strobel D. An abdominal and thyroid status with Acoustic Radiation Force Impulse Elastometry: a feasibility study: Acoustic Radiation Force Impulse Elastometry of human organs. Eur J Radiol 2011;80:e226–e230.
2. Mei M, Ni J, Liu D, Jin P, Sun L. EUS elastography for diagnosis of solid pancreatic masses: a meta-analysis. Gastrointest Endosc 2013;77:578–589.
3. Rustemovic N, Cukovic-Cavka S, Brinar M, Radic D, Opacic M, Ostojic R, et al. A pilot study of transrectal endoscopic ultrasound elastography in inflammatory bowel disease. BMC Gastroenterol 2011;11:113.
4. Stock KF, Klein BS, Vo Cong MT, Sarkar O, Romisch M, Regenbogen C, et al. ARFI-based tissue elasticity quantification in comparison to histology for the diagnosis of renal transplant fibrosis. Clin Hemorheol Microcirc 2010;46:139–148.
5. Barrault C, Roudot-Thoraval F, Tran Van Nhieu J, Atanasiu C, Kluger MD, Medkour F, et al. Non-invasive assessment of liver graft fibrosis by transient elastography after liver transplantation. Clin Res Hepatol Gastroenterol 2013;37:347–352.
6. Woo S, Kim SY, Cho JY, Kim SH. Shear wave elastography for detection of prostate cancer: a preliminary study. Korean J Radiol 2014;15:346–355.
7. D'Anastasi M, Schneevoigt BS, Trottmann M, Crispin A, Stief C, Reiser MF, et al. Acoustic radiation force impulse imaging of the testes: a preliminary experience. Clin Hemorheol Microcirc 2011;49:105–114.
8. Molina FS, Gomez LF, Florido J, Padilla MC, Nicolaides KH. Quantification of cervical elastography: a reproducibility study. Ultrasound Obstet Gynecol 2012;39:685–689.
9. Gennisson JL, Deffieux T, Mace E, Montaldo G, Fink M, Tanter M. Viscoelastic and anisotropic mechanical properties of in vivo muscle tissue assessed by supersonic shear imaging. Ultrasound Med Biol 2010;36:789–801.
10. Ahn KS, Kang CH, Hong SJ, Jeong WK. Ultrasound elastography of lateral epicondylosis: clinical feasibility of quantitative elastographic measurements. AJR Am J Roentgenol 2014;202:1094–1099.
11. Trahey GE, Palmeri ML, Bentley RC, Nightingale KR. Acoustic radiation force impulse imaging of the mechanical properties of arteries: in vivo and ex vivo results. Ultrasound Med Biol 2004;30:1163–1171.
12. Dumont D, Dahl J, Miller E, Allen J, Fahey B, Trahey G. Lower-limb vascular imaging with acoustic radiation force elastography: demonstration of in vivo feasibility. IEEE Trans Ultrason Ferroelectr Freq Control 2009;56:931–944.
13. Ghajarzadeh M, Sodagari F, Shakiba M. Diagnostic accuracy of sonoelastography in detecting malignant thyroid nodules: a systematic review and meta-analysis. AJR Am J Roentgenol 2014;202:W379–W389.
14. Zengel P, Schrotzlmair F, Schwarz F, Paprottka P, Kramer M, Berghaus A, et al. Elastography: a new diagnostic tool for evaluation of obstructive diseases of the salivary glands; primary results. Clin Hemorheol Microcirc 2012;50:91–99.
15. Mansour N, Stock KF, Chaker A, Bas M, Knopf A. Evaluation of parotid gland lesions with standard ultrasound, color duplex sonography, sonoelastography, and acoustic radiation force impulse imaging: a pilot study. Ultraschall Med 2012;33:283–288.
16. Barr RG, Nakashima K, Amy D, Cosgrove D, Farrokh A, Schafer F, et al. WFUMB guidelines and recommendations for clinical use of ultrasound elastography: Part 2: breast. Ultrasound Med Biol 2015;41:1148–1160.
17. Ferraioli G, Filice C, Castera L, Choi BI, Sporea I, Wilson SR, et al. WFUMB guidelines and recommendations for clinical use of ultrasound elastography: Part 3: liver. Ultrasound Med Biol 2015;41:1161–1179.
18. Cosgrove D, Piscaglia F, Bamber J, Bojunga J, Correas JM, Gilja OH, et al. EFSUMB guidelines and recommendations on the clinical use of ultrasound elastography. Part 2: Clinical applications. Ultraschall Med 2013;34:238–253.
19. Palmeri ML, Nightingale KR. What challenges must be overcome before ultrasound elasticity imaging is ready for the clinic? Imaging Med 2011;3:433–444.
20. Nightingale K, Soo MS, Nightingale R, Trahey G. Acoustic radiation force impulse imaging: in vivo demonstration of clinical feasibility. Ultrasound Med Biol 2002;28:227–235.
21. Lazebnik RS. Tissue strain analytics: virtual touch tissue imaging and quantification. ACUSON S2000 Ultrasound System. ACUSON S2000 Ultrasound System. Mountain View, CA: Siemens Medical Solutions, 2008.
22. John B, Liexiang F. Understanding ARFI and new elastography quantification technologies. Mountain View, CA: Siemens Medical Solutions, 2014.
23. Lupsor M, Badea R, Stefanescu H, Sparchez Z, Branda H, Serban A, et al. Performance of a new elastographic method (ARFI technology) compared to unidimensional transient elastography in the noninvasive assessment of chronic hepatitis C: preliminary results. J Gastrointestin Liver Dis 2009;18:303–310.
24. Yamanaka N, Kaminuma C, Taketomi-Takahashi A, Tsushima Y. Reliable measurement by virtual touch tissue quantification with acoustic radiation force impulse imaging: phantom study. J Ultrasound Med 2012;31:1239–1244.
25. Shin HJ, Kim MJ, Kim HY, Roh YH, Lee MJ. Comparison of shear wave velocities on ultrasound elastography between different machines, transducers, and acquisition depths: a phantom study. Eur Radiol 2016 Jan 26 [Epub]. http://dx.doi.org/10.1007/s00330-016-4212-y.
26. Potthoff A, Attia D, Pischke S, Kirschner J, Mederacke I, Wedemeyer H, et al. Influence of different frequencies and insertion depths on the diagnostic accuracy of liver elastography by acoustic radiation force impulse imaging (ARFI). Eur J Radiol 2013;82:1207–1212.
27. Friedrich-Rust M, Wunder K, Kriener S, Sotoudeh F, Richter S, Bojunga J, et al. Liver fibrosis in viral hepatitis: noninvasive assessment with acoustic radiation force impulse imaging versus transient elastography. Radiology 2009;252:595–604.
Principle of acoustic radiation force impulse quantification.An acoustic push pulse (longitudinal wave) generates minimal deformation of the tissue, inducing shear waves in a user-defined region of interest, which propagate in a perpendicular direction (transversal waves). By applying tracking beams in multiple locations and revealing arrival time, we can quantify the shear wave propagation speed. This correlates closely to the tissue stiffness [22].
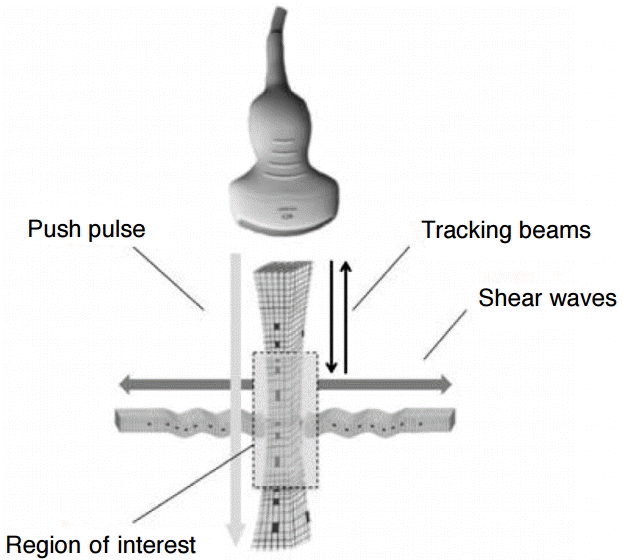 Fig. 1.Experimental set-up.A, B. Actual set-up (A) and simplified diagram of the set-up (B) are shown. The probe (a) is held by a supporting arm (b). The phantom (c) contains four spherical lesions (diameter: 20 mm, at a depth of 35 mm) of different, defined stiffness values (7.3 kPa, 18.8 kPa, 45.9 kPa, and 61.5 kPa). It is positioned on a digital weighing scale (d).
 Fig. 2.Example of the 50% intralesional positioning of the region of interest (ROI).The ROI is positioned in such a way that it is partly filled by one of the lesions and partly by the background of the phantom.
 Fig. 3.Measured shear wave velocity (SWV) versus reference value (including all measurements).The scatter points lie close to the reference line (=non-continuous line), suggesting a high correlation between the measured SWV and the reference value. The interpolants for each probe (=continuous lines) show different patterns: the SWV values from the convex probe end to lie closer to the reference value, whereas the SWV values by the linear probe seem be more frequently underestimated.
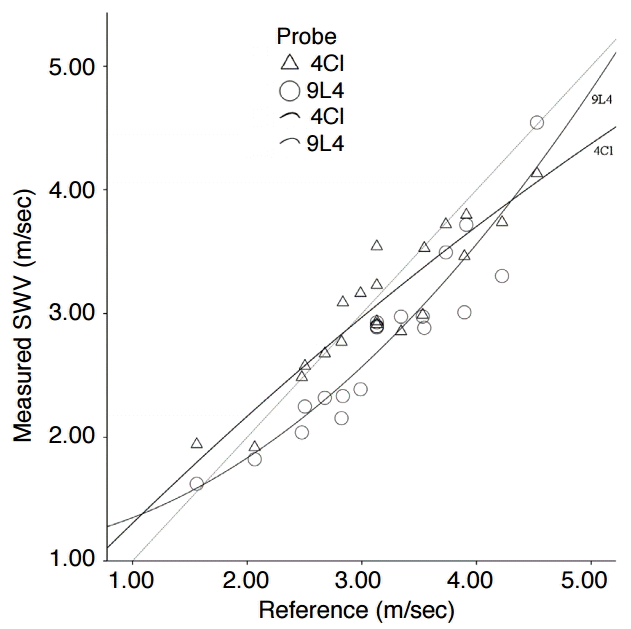 Fig. 4.Table 1.Measured values for a comparison of the 4C1 and 9L4 probes
Descriptive parameters and results from the t test are shown. The measurements of all lesions are averaged. Group 1 concludes all measurements (i.e., shear wave velocity in all lesions, under each condition), group 2 includes the series in which the ROI was positioned 0% or 100% in a spherical lesion, and group 3 includes the series in which the ROI was placed 25%, 50%, and 75% in the spherical lesion. SD, standard deviation; Abs_D, absolute difference of the reference value minus the measured value; ROI, region of interest. Table 2.Comparison of the positioning of the ROI in structure(s) having homogenous versus heterogeneous elastic properties: absolute mean, SD, and validity of the SWV
Descriptive parameters and results from the t test are shown. The measurements of all lesions are averaged. Group 2 includes the series in which the ROI was positioned 0% or 100% in a spherical lesion, and group 3 includes the series in which the ROI was placed 25%, 50%, and 75% in the spherical lesion. ROI, region of interest; SD, standard deviation; SWV, shear wave velocity; Abs_D, absolute difference of the reference value minus the measured value. |



 Print
Print facebook
facebook twitter
twitter Linkedin
Linkedin google+
google+
 Download Citation
Download Citation PDF Links
PDF Links PubReader
PubReader ePub Link
ePub Link Full text via DOI
Full text via DOI Full text via PMC
Full text via PMC




