AbstractThis review aimed to describe the state of the art in muscle-tendon unit (MTU) assessment by supersonic shear wave imaging (SSI) elastography in states of muscle contraction and stretching, during aging, and in response to injury and therapeutic interventions. A consensus exists that MTU elasticity increases during passive stretching or contraction, and decreases after static stretching, electrostimulation, massage, and dry needling. There is currently no agreement regarding changes in the MTU due to aging and injury. Currently, the application of SSI for the purpose of diagnosis, rehabilitation, and physical training remains limited by a number of issues, including the lack of normative value ranges, the lack of consensus regarding the appropriate terminology, and an inadequate understanding of the main technical limitations of this novel technology.
The muscle-tendon unit (MTU) involves the connection between the muscles and tendons, through which contractile forces are generated and transmitted. Muscle fibers not only transmit force to tendons, but also interact with them due to their mechanical properties [1].
Supersonic shear wave imaging (SSI) is a dynamic method with proven superiority in the evaluation of the mechanical properties of tissue due to the high-resolution images it provides of superficial and deep tissues, and because it provides local quantitative elastic data in an ultrafast way. For these reasons, SSI has attracted attention from technical and clinical researchers for the diagnosis of liver fibrosis [2,3], breast tumors [4,5], and thyroid lesions [6], as well as the assessment of placental elasticity in preeclampsia [7].
In recent years, the use of SSI elastography in biomechanics research has expanded, and it now has potential applications in rehabilitation and physical training. However, the elastography results of biomechanics studies have not been established as well as they have been in clinical fields. To date, several papers have been published with different methodological parameters, making a universal interpretation of the results difficult [8-11].
Therefore, the aim of this review was to describe the state of the art in SSI elastography and its use in evaluating the mechanical properties of muscles and tendons during contraction and stretching, after injury, during aging, and in response to other stressors.
The terminology used to describe the mechanical and acoustic properties of biological tissue can be confusing, so this subsection presents these properties and their definitions, in order to facilitate an understanding of the text. It is important to note that many papers use the terms stiffness, elasticity, and/or hardness to represent Young’s modulus [12-15]. The definitions of the mechanical and acoustic properties discussed in this study are presented in Table 1 [16,17].
The dynamic elastography method known as SSI was developed 12 years ago. The ultrasound system operates in two modes: pushing (Fig. 1A) and imaging (Fig. 1B). Initially, the imaging mode is used to collect a reference image of the medium. In the pushing mode, an electronically focused transducer generates an acoustic radiation force at distinct and successive depths. Consequently, cylindrical shear wave sources are created and their constructive interference forms the Mach cone (Fig. 1A), which represents the propagation of two quasi-planar shear wave fronts in opposite directions. The transducer then returns to the imaging mode (Fig. 1B) and is excited by sinusoids with 3 to 6 kHz (3,000 to 6,000 images per second) of pulse repetition to detect the vibration of the medium in response to the propagation of the shear wave [18,19]. It is now is possible to generate frequencies up to 30 kHz (30,000 images per second) in order to study thin structures such as the cornea and arteries.
Image processing consists of applying the cross-correlation algorithm to all of the images acquired after pushing and to the reference image. This process is used to determine the degree of medium displacement due to propagation of the shear wave. From the images of the wave displacement over time, it is possible to obtain the shear modulus (μ) of the medium [20,21].
In biological tissue, a shear wave induces particle movement perpendicularly to the direction of wave propagation with a speed of approximately a few meters per second (less than 30 m/sec) [16]. For a purely elastic and isotropic medium, the shear wave speed (cs) is directly related to the shear modulus: μ=pcs2 [16], where p is the biological tissue density (1,000 kg/m3). For incompressible media, including most biological tissues, μ is approximately one-third of the Young’s modulus (μ=E/3). Therefore, assuming a purely elastic medium, the shear wave speed can be used to obtain the Young’s modulus according to E=3pcs2 [22], which means that the values of the Young's modulus increase as the shear wave speed increases. Fig. 2 shows an example of an elastographic image with the Young’s modulus value.
Table 2 summarizes the main advantages and limitations of ultrasound elastography methods [12,23]. It also shows the parameters obtained with each method/equipment and the corresponding vibration source used.
SSI has several advantages over quasi-static elastography techniques, including greater reproducibility on account of the fact that it is less examiner-dependent, the ability to produce more quantitative data, reliance on automatic shear wave generation, and the provision of good elasticity contrast. In addition, shear waves can be generated at depths where manual compression to produce tissue strain is not possible or is ineffective [24].
Additionally, SSI has advanced the field of elastography, as it provides tissue elastic information in real time with superimposed B-mode images (unlike FibroScan), high-resolution images of superficial or deep tissues, and greater ease of equipment handling.
In biomechanics, SSI allows researchers to examine the MTU in dynamic states (such as contraction) and allows an assessment of hard tissue (such as tendons) since it can assess a wide range of Young’s modulus values (from 0 to 800 kPa; shear wave speed=16.33 m/sec). This is in contrast to other equipment such as the ACUSON S3000 (Siemens, Erlangen, Germany), which only allows a maximum shear wave velocity of 8.4 m/sec (Young’s modulus=211.68 kPa), thus limiting its biomechanical application.
Acoustic radiation force methods (SSI and acoustic radiation force imaging [ARFI]) allow investigators to select the shear wave region by adjusting the focal depth of the transducer. The region of interest (ROI) in ARFI imaging is very small when compared to SSI. The ROI size in Aixplorer (SSI) can be adjusted according to the user's interest: 4×2 cm for the tendon preset and 3×2.5 cm for the muscle preset. The Q-box (quantitative information) has a maximum diameter of 25 mm. SSI is not without its limitations, including a high cost and low shear wave amplitude, which can cause a loss of wave energy.
The relation between E or μ values and muscle force has been the focus of a series of studies that monitored the changes of these values during muscle contraction.
E in the tibialis anterior (TA), gastrocnemius medialis (GM), and soleus (Sol) muscles was measured during isometric plantar and dorsiflexion contraction from rest to 30% of maximal voluntary contraction (MVC) in a single subject (Fig. 3). With the knee fully extended, E values increased (40.60±1.00 to 258.10±15.00 kPa for the TA, 16.50±1.00 to 225.40±41.00 kPa for the GM, and 14.50±2.00 to 55.00±5.00 kPa for Sol). During knee flexion, E increased less in the GM than in Sol: 41.20±2.00 versus 76.80±7.00 kPa, respectively [31]. As a bi-articular muscle, the length of the gastrocnemius is optimized with the knee extended.
Bouillard et al. [32] correlated μ with data obtained from electromyography and with torque values (from 0 to 60% of MVC) in order to assess the hand muscle strength of 11 young men. The μ value was a more accurate estimate of strength (R2 =0.98±0.01) than electromyography (R2 =0.94±0.03) [32]. Yoshitake et al. [33] evaluated the μ value of the biceps brachii muscle in 10 healthy subjects at rest and during submaximal contraction (15%, 30%, 35%, and 60% of MVC). The results showed a significant linear increase in μ with the contraction intensity and good μ value reliability: the intraclass correlation coefficient (ICC) intrasession was 0.97 and intersession 0.90. The authors highlighted the use of elastography to estimate the contraction intensity of deep muscles, which is a limitation of surface electromyography [33]. Maximal contractions (0 to 100% MVC) were investigated in the abductor digiti minimi of the hand of 10 healthy subjects. The R2 ranged from 0.86 to 0.98, showing a quasilinear relationship between μ and torque, as well as good reliability. The ICC ranged from 0.73 to 0.98 for two repeated contractions at each intensity [34].
The influence of muscle fatigue on μ was investigated in 16 healthy individuals. Electrostimulation was used to selectively fatigue the vastus lateralis muscle. Knee extension sustained at 20% of MVC until failure was tested before and after stimulation. There was a significant reduction of torque (from 273.9±67.3 to 226.2±72.7 kPa) and vastus lateralis μ in the electrostimulation group compared to the control group (54.6±11.8 kPa vs. 68.4±19.2 kPa, respectively; P=0.011). There was no change in μ in other muscles, showing that load sharing among agonists did not occur after vastus lateralis fatigue [35].
In summary, E or μ values have been found to increase at submaximal and maximal contractions and to decrease in states of fatigue. Considering the good reliability of these findings, elastography would appear to provide a direct estimation of muscle force.
Passive stretching involves MTU lengthening, promoted by submaximal joint mobilization usually on an isokinetic dynamometer. Passive torque or stiffness increases with MTU lengthening due to the resistance of the periarticular structures such as the conjunctive tissue, joint capsule, and ligaments. In contrast, MTU relaxation (slack length) occurs at very short lengths or within the physiological range of lengths (i.e., between the smallest and greatest lengths in vivo) [36].
A significant increase was found in the E of the Achilles tendon from maximal plantar flexion to dorsiflexion in 80 healthy individuals (147.60±62.60 to 779.50±57.10 kPa for the sagittal plane and 78.70±26.90 to 266.10±13.70 kPa for the axial plane). However, the reliability was poor (-0.01 to 0.46), probably due the difficulty in ensuring the mapping of the same region at all ankle angles [37]. Similarly, Hug et al. [38] demonstrated an increase in μ with dorsiflexion. They also defined the ankle angle, which represents the GM slack length (the length at which the tissue begins to develop passive tension) during passive ankle mobilization from 50° of plantar flexion to 80% maximum dorsiflexion at two knee angles (0° for extension and 90° for flexion). The ankle angle corresponding to the GM slack length with the knee fully extended (-24.3°±5.8°) was significantly more plantarflexed than with the knee flexed at 90° (-16.8°±5.2°). For the Achilles tendon, the ankle angle corresponding to the slack length was similar in both knee positions (fully extended, -43.7°±3.2°; the knee flexed at 90°, -42.3°±4.9°). On account of its greater stiffness, an increase in tension is more easily verified in the tendon than in the muscle [38].
In another study, the shear elastic modulus of the GM was monitored during passive dorsiflexion with the knee at an angle of 0° and flexed to 15°, 30°, 45°, 60°, and 80° in a group of seven subjects. As expected, μ increased with passive dorsiflexion, and the slack length of the gastrocnemius corresponded to 20°±4º of plantarflexion (knee fully extended) [26]. Lacourpaille et al. [39] assessed the slack length of the biceps brachii muscle (two heads) in 12 healthy men, and showed an increase in μ with elbow extension. The slack length of the long and short heads occurred at 95.50°±6.30° and 95.30°±8.20°, respectively [39]. A similar study was carried out in healthy TA muscles, with a protocol of two consecutive cycles of 50° plantar flexion to 15° dorsiflexion (or -15° of plantar flexion). The reliability of the μ values was considered to be good, with a coefficient of variation ranging from 0.82 to 3.26. The mean TA slack length was 10.90°±6.30° with an ICC of 0.85 [40].
The E values of the GM and Achilles tendon among 25 healthy subjects were evaluated at an ankle angle of 0º and their correlation with passive ankle stiffness was assessed, as determined by the joint angle-passive torque relationship. There was no significant relationship between muscle or tendon E and passive joint stiffness (r=-0.37, P=0.07 and r=-0.39, P=0.052, respectively). However, the GM and Achilles tendon stiffness index, acquired by the displacement of the muscle-tendon junction in a B-mode image, had a better correlation with passive joint stiffness (r=0.80, P<0.001 and r=0.60, P<0.002, respectively). According to the authors, passive joint stiffness was associated with variations in the elasticity of the proximal and distal aponeurosis and the proximal tendon of the GM, as well as the ligaments and joint capsule of the ankle. Chino and Takahashi [41] did not apply elastography to evaluate these structures, which explains the weak correlation.
Changes in μ in bi-articular muscles such as the hamstrings were investigated by Le Sant et al. [42] during passive muscle lengthening in 18 individuals (Fig. 4). The μ of the hamstrings increased up to 110° of hip flexion with the knee extended (maximal μ: 62.3±22.0 kPa for the semitendinosus, 69.9±17.8 kPa for the semimembranosus, and 77.8±20.5 kPa for the biceps-femoris long head [BF]) and to a lesser degree when the hip was flexed at 70° (30.3±11.2 kPa for the semitendinosus, 38.3±10.0 kPa for the semimembranosus, and 33.3±9.8 kPa for the BF) and 90° (45.8±18.7 kPa for the semitendinosus, 60.6±17.0 kPa for the semimembranosus, and 59.2±15.2 kPa for the BF). The individual muscle analysis showed the highest μ values for the BF (32.6±21.6 kPa), in contrast to the semimembranosus (27.8±17.2 kPa) and semitendinosus (22.9±15.6 kPa), probably due to differences in cross-sectional area, specific tension, the degree of anisotropy, and the passive muscle force-length relationship [42]. Umehara et al. [43] investigated the effect of 3 hip rotations (neutral, internal, and external) and four knee angles (0°, 45°, 90°, and 135°) on the μ of the bi-articular tensor fasciae lata during a stretching maneuver (hip adduction and extension). The tensor fasciae lata μ in each stretch position was greater than in the neutral and relaxed joint position. The best stretching posture was identified as being with the hip in an adducted and extended position with knee angles of 90° and 135°, as the shear elastic modulus was significantly greater than at 0° and 45° [43]. Dubois et al. [44] reported the results of a reliability study that compared 11 lower limb muscles at rest and during stretching. The intraoperator coefficient of variation ranged from 7% to 24% and the interoperator coefficient of variation ranged from 5% to 15% at rest and in stretching positions. The lower reliability of the soleus and biceps femoris muscles was attributed to their deeper location and thinner structure, respectively. For all muscles tested, the value of μ increased with stretching [44].
In conclusion, previous studies have shown an increase in the shear modulus as the MTU lengthened, thereby highlighting the potential of elastography to estimate the passive tension pattern of muscles and tendons.
Static stretching is an exercise applied to promote gains in range of motion. In the studies presented in this section, elastography acquisitions were made in resting muscles, after the application of a static stretching protocol.
Multiple studies have investigated the effect of static stretching on E and μ values [27,28,30,45]. Two independent research groups [27,28] studied the E values of the GM and gastrocnemius lateralis (GL) muscles. After a session involving three series of ankle dorsiflexion static stretching over a period of 2 minutes, there was a significant reduction in the E value (from 27.60±7.30 to 24.00±5.80 kPa and from 33.50±6.30 to 29.20±5.80 kPa for the GM and GL, respectively). The lower GM E value persisted even after stretching, suggesting that static stretching affected both muscles in the same way [27]. Similar results were obtained in another study conducted by the same group, which consisted of a more exhaustive exercise program that was conducted over the course of 6 weeks. Nineteen young men were recruited into the study and required to perform 2 minutes of static ankle stretching 5 times weekly. Compared to the control contralateral limb, there was a reduction in E in both muscles (from 27.30±7.30 to 24.40±5.40 kPa and from 32.40±5.80 to 30.00±4.40 kPa, for the GM and GL, respectively) [28]. Taniguchi et al. [45] tested a static stretching protocol (five sets of 1 minute) in the gastrocnemii of 10 healthy subjects. They found a 14% (1.18 kPa) reduction in the μ value in both muscles. However, these changes returned to baseline after 20 minutes, demonstrating the transient effect of a single stretching session on the muscle tissue [45]. Using the same protocol, the hamstring muscles were stretched with the knee at 90° flexion (slack position) and at 45° of flexion. Prior to performing the maneuver and with the knee in 45° of flexion, the μ of the semitendinosus (42.2±10.7 kPa) was significantly lower than that of the semimembranosus (108.2±28 kPa) and biceps femoris (72.4±20.2 kPa). After static stretching, μ decreased in all muscles, but the decrease was especially notable for the semimembranosus at 45° of flexion at the knee (74.2±19.8 kPa) [30].
In summary, although the μ of the MTU increased during lengthening, there appears to be a decrease in μ after static stretching. However, more studies are necessary to investigate the long-term effects of stretching. These studies open the door to a yet unexplored field of research, which aims to understand changes in individual muscle elasticity in response to stretching of the corresponding muscle group. This knowledge would be invaluable for the practice of rehabilitation.
Elastography has also been applied to determine the effects of therapeutic techniques such as massage and dry needling.
Crommert et al. [46] performed a 7-minute massage protocol on the GM muscle (Fig. 5) and found an immediate reduction in the μ value of the massaged leg compared to baseline (from 11.0±3.1 to 10.3±2.6 kPa, P=0.01), but this effect was not sustained after 3 minutes (10.9±2.8 kPa), indicating that the selected massage protocol had a very short effect [46].
Dry needling is an invasive technique that produces small-scale tissue injuries in order to provide pain relief and reduce the tissue stiffness of muscles with trigger points. In seven women suffering from the latter set of symptoms, dry needling produced a significant reduction in the μ of the upper trapezius muscle (from 13.56 to 9.11 kPa and 10.23 to 7.67 kPa in sitting and prone positions, respectively) [47].
In summary, changes in E or μ in response to massage and dry needling are similar to those seen with stretching (i.e., a decrease of E or μ). Clinicians and physiotherapists could apply these techniques to promote the relaxation of stiff muscles and increase the range of motion, as well as to aid pain relief. However, more studies are necessary to confirm these responses.
As part of the normal aging process, muscles and tendons undergo structural changes, which alter the mechanical properties of the MTU and ultimately affect function. Elastography is a potentially useful technique to monitor these changes.
Hsiao et al. [8] found a 28% to 36% reduction in the E of the patellar tendon in older individuals (176.2±45.9 kPa) compared to young (243.1±61.4 kPa) and middle-aged (238.7±73.7 kPa) individuals. They attributed this difference to the loss of collagen fiber organization and tissue metaplasia. Additionally, they pointed out that other factors such as physical activity can also influence the mechanical aging process of tissues [8].
The influence of age and gender on the μ value of the biceps brachii muscle was studied in 133 healthy subjects aged 21 to 94 years old. In the elderly group (>60 years old), there was a significant positive trend in the relationship between shear modulus and age, reflecting increased biceps brachii stiffness with age. Gender also influenced elasticity, as μ values tended to be higher for females than for males after controlling for age. However, the lower number of men than women in each decade group may have reduced the statistical power of this study [9].
The mean elasticity E values for some muscles and tendons were investigated in 127 healthy volunteers from 17 to 63 years old. There was no group of elderly subjects (more than 65 years old). The E values were 11.10±4.10, 10.40±3.70, 31.20±13.00, 74.40±45.70, and 51.50±25.10 kPa for the gastrocnemius and masseter muscles, supraspinatus, and Achilles tendons (longitudinal and transverse planes), respectively. The E of the Achilles tendon was greater in men than in women. There was no significant correlation between age (up to 63) and E for any structure [25].
The few studies cited above are insufficient to allow universal conclusions to be drawn regarding the relationship between age and the MTU shear modulus. Further research is needed to improve our understanding of this field.
Aubry et al. [48] investigated the shear wave speed of normal and pathologic Achilles tendons in two ankle positions (relaxed and maximal plantar flexion) and two orientations of the probe (sagittal and axial to the collagen fibers) (Fig. 6). Higher shear wave speed represents an increase of the μ or E of the tissue. Achilles tendons with midportion tendinopathy (n=24) had significant lower shear wave speeds than normal tendons (n=180) in both relaxed and stretched positions, reflecting less stiff tissue. In the relaxed ankle position, mean velocities lower than 4.06 m/sec (axial plane; 54.2% sensitivity and 91.5% specificity) and 5.7 m/sec (sagittal plane; 41.7% sensitivity and 81.8% specificity) were considered signs of tendinopathy. The authors concluded that elastography was a useful tool for quantifying pathologic tendon shear wave speed, with high specificity but relatively low sensitivity [48].
Botanlioglu et al. [29] compared the mechanical properties of the vastus medialis oblique (VMO) muscle during periods of rest and isometric contraction in three groups: 11 healthy men, 11 healthy women, and 11 women with patellofemoral pain syndrome (measured by a score ≥3 cm on a 10-cm visual analog scale, assessed after functional activities). The VMO elasticity and VMO contraction ratio (elasticity at contraction to elasticity at rest) were significantly lower in women with patellofemoral pain than in women in the control group (from 13.0±3.3 to 103.9±39.3 kPa vs. 12.1±3.5 to 157.6±31.0 kPa, at rest and in contraction, respectively) [29].
The biceps brachii shear wave speed was compared between the nonparetic and paretic sides of 16 stroke survivors. The shear wave speed was 69.5% greater in paretic muscle than nonparetic muscle (Cs=3.67±1.28 m/sec vs. 2.23±0.40 m/sec; P<0.001). Furthermore, there was a significant linear correlation between the difference in shear speed of the two sides and the time from stroke (R2 =0.301, P=0.03). The greater shear wave speed in paretic muscle can be explained by the increased content of collagen, titin protein, and extracellular matrix [49].
Muscle damage was studied in the posterior thigh muscles of 28 rabbits subjected to pressure damage. E values were collected before the formation of the lesion and 0.5, 2, 6, 24, and 72 hours afterwards. The results showed a significant E increase from baseline (6.78±2.06 kPa) to 12.44±3.77 kPa at 0.5 hours, 13.20±3.60 kPa at 2 hours, 10.04±2.95 kPa at 24 hours, and 9.72±3.90 kPa at 72 hours, which corresponded approximately to the recovery level. When the muscles were analyzed histopathologically, researchers noted an increase in vascularity, myocyte size, and the amount of interstitial fluid until 6 hours postdecompression. After 6 hours after the decompression, the greater stiffness was explained by the action of an intense inflammatory process, with a large number of white cells and a large amount of exudate [11].
Another study applied a heavy eccentric exercise protocol for the elbow flexor muscles in 16 healthy subjects. After 1 hour of exercise, there was a significant increase in μ (from 7.2±1.2 to 11.0±2.4 kPa for the medial biceps brachii and 7.5±1.6 to 10.5±2.8 kPa for the brachialis at an elbow angle of 110°), which corresponded to the onset of delayed onset muscle soreness, as assessed by a subjective scale. After 48 hours and 21 days, the μ values were similar to baseline (Fig. 7). The transient μ increase may be explained by a disturbance in calcium homeostasis, which results in a higher number of active muscle cross-bridges and, consequently, higher levels of activation. This is in accordance with reports of elevated intramuscular calcium during periods of active stretching (eccentric contraction) due to the increased sensitivity of muscle sarcomeres [50].
In summary, increased elasticity has been observed in paretic muscles and in damaged muscles. However, tendinopathy and patellofemoral pain syndrome cause a reduction in tissue elasticity. Despite these conflicting results, elastography is a useful tool for diagnosing and following up injuries, and could be an adjunct to subjective methods such as palpation.
For an SSI examiner, technical information is necessary as a guideline. The standardization of some parameters such as ROI size, time acquisition, and manual pressure are important to avoid acquisition errors and conflicting results between studies.
Different transducer pressures, ROI sizes, and image acquisition times were compared in terms of their effects on rectus femoris muscle and patellar tendon elasticity values. The elastic modulus values increased significantly (Fig. 8) with higher transducer pressures (32.39±14.17 kPa and 134.57±73.75 kPa for the muscle and tendon, respectively), emphasizing the importance of controlling these variables during image acquisition [51].
The influence of the ROI size on the μ value was tested in the abductor digiti minimi muscle of 10 males. The relative error of μ increased with decreasing ROI size (full ROI in the largest region of the muscle, 1/2, 1/4, and 1/6 ROI), demonstrating the spatial variability of the shear elastic modulus. It is advisable to calculate the μ over the greatest possible ROI or to average several ROIs [34].
Muscles and tendons exhibit anisotropic behavior; that is, the speed of shear wave propagation may change depending on the orientation (parallel or transversal) of the muscle or tendon fibers [52,53]. It is important to standardize the probe position in relation to the structure of interest. In order to obtain more accurate measurements, it is recommended to align the probe with the muscle/tendon fibers [54,55], since the forces transmitted to the tissue will follow the fibers’ direction [55]. Furthermore, dispersive and viscosity effects will be avoided [52].
In summary, we recommend the standardization of the acquisition protocol, and suggest that investigators use slight transducer pressure, the largest ROI possible, and align the probe with the fibers. Although image acquisition time does not influence elasticity values [51], some time is required for elastography map stabilization.
Multiple authors [8,33,34,40] have reported that elastography is a reliable tool to assess tissue elasticity, although some studies did not report the reliability of the measurements intra or intersessions [11,28,30,34,40,52]. It is also important to remember that there is individual biological variability in elasticity values and that these must be taken into account when attempting to establish a normative data range for muscle and tendon tissues. In this context, the majority of the studies cited above included 15 to 20 individuals. Larger groups of close to 100 subjects were reported in three studies [9,25,37]. Large sample sizes are necessary to obtain tissue elasticity reference data.
Tendon structures have been less thoroughly studied than muscles. This discrepancy can be partly explained by the technical limitations of the methods used. When the SSI principle is applied to thin structures, another kind of wave is generated (guided waves [53]), which can introduce a source of error. Additionally, shear waves propagate much faster in harder structures, which can cause a saturation of the E values shown on the equipment. For tendons with these characteristics (thin and stiff), both of these problems can occur. Subsequent work must be done in order to overcome these limitations in the newer versions of current equipment.
Twenty-nine papers were described in this review. Different nomenclature has been used to refer to tissue elasticity, including hardness, elastic modulus, elasticity values, shear elastic modulus and the Young’s modulus. This inconsistency highlights the need for a standardization of the terminology used to describe the mechanical properties of tissues. We recommend the use of the term shear elastic modulus, which is obtained by dividing the Young’s modulus by 3. Readers should take care with these terms to avoid the misinterpretation of elastography variables and to improve their understanding of the results obtained by different studies.
This review discussed the state of the art of SSI elastography as an emerging technique for measuring the mechanical properties of muscles and tendons. A consensus exists that MTU elasticity increases during passive stretching or contraction, and reduces after static stretching, electrostimulation, massage, and dry needling. There is currently no agreement regarding changes in the MTU during the aging process and in response to injury.
Before this technique can be used routinely for diagnosis, rehabilitation, and physical training, further work must be done in order to establish normative data, reach a consensus regarding the terminology used by researchers and clinicians, and further elucidate the technical limitations of this novel technology.
References1. Fukunaga T, Kawakami Y, Kubo K, Kanehisa H. Muscle and tendon interaction during human movements. Exerc Sport Sci Rev 2002;30:106–110.
2. Bavu E, Gennisson JL, Couade M, Bercoff J, Mallet V, Fink M, et al. Noninvasive in vivo liver fibrosis evaluation using supersonic shear imaging: a clinical study on 113 hepatitis C virus patients. Ultrasound Med Biol 2011;37:1361–1373.
3. Cha SW, Jeong WK, Kim Y, Kim MY, Kim J, Kim SY, et al. Nondiseased liver stiffness measured by shear wave elastography: a pilot study. J Ultrasound Med 2014;33:53–60.
4. Chang JM, Moon WK, Cho N, Yi A, Koo HR, Han W, et al. Clinical application of shear wave elastography (SWE) in the diagnosis of benign and malignant breast diseases. Breast Cancer Res Treat 2011;129:89–97.
5. Berg WA, Cosgrove DO, Dore CJ, Schafer FK, Svensson WE, Hooley RJ, et al. Shear-wave elastography improves the specificity of breast US: the BE1 multinational study of 939 masses. Radiology 2012;262:435–449.
6. Szczepanek-Parulska E, Wolinski K, Stangierski A, Gurgul E, Biczysko M, Majewski P, et al. Comparison of diagnostic value of conventional ultrasonography and shear wave elastography in the prediction of thyroid lesions malignancy. PLoS One 2013;8:e81532.
7. Kilic F, Kayadibi Y, Yuksel MA, Adaletli I, Ustabasioglu FE, Oncul M, et al. Shear wave elastography of placenta: in vivo quantitation of placental elasticity in preeclampsia. Diagn Interv Radiol 2015;21:202–207.
8. Hsiao MY, Chen YC, Lin CY, Chen WS, Wang TG. Reduced patellar tendon elasticity with aging: in vivo assessment by shear wave elastography. Ultrasound Med Biol 2015;41:2899–2905.
9. Eby SF, Cloud BA, Brandenburg JE, Giambini H, Song P, Chen S, et al. Shear wave elastography of passive skeletal muscle stiffness: influences of sex and age throughout adulthood. Clin Biomech (Bristol, Avon) 2015;30:22–27.
10. Le Sant G, Nordez A, Andrade R, Hug F, Freitas S, Gross R. Stiffness mapping of lower leg muscles during passive dorsiflexion. J Anat 2017;230:639–650.
11. Lv F, Tang J, Luo Y, Ban Y, Wu R, Tian J, et al. Muscle crush injury of extremity: quantitative elastography with supersonic shear imaging. Ultrasound Med Biol 2012;38:795–802.
12. Sarvazyan A, Hall TJ, Urban MW, Fatemi M, Aglyamov SR, Garra BS. An overview of elastography: an emerging branch of medical imaging. Curr Med Imaging Rev 2011;7:255–282.
14. Parker KJ, Doyley MM, Rubens DJ. Imaging the elastic properties of tissue: the 20 year perspective. Phys Med Biol 2011;56:R1–R29.
15. DeWall RJ, Slane LC, Lee KS, Thelen DG. Spatial variations in Achilles tendon shear wave speed. J Biomech 2014;47:2685–2692.
16. Cobbold RS. Foundations of biomedical ultrasound. New York: Oxford University Press, 2007.
17. Hoskins PR, Martin K, Thrush A. Diagnostic ultrasound: physics and equipment. 2nd ed. Cambridge: Cambridge University Press, 2010.
18. Bercoff J, Chaffai S, Tanter M, Sandrin L, Catheline S, Fink M, et al. In vivo breast tumor detection using transient elastography. Ultrasound Med Biol 2003;29:1387–1396.
19. Bercoff J, Tanter M, Fink M. Supersonic shear imaging: a new technique for soft tissue elasticity mapping. IEEE Trans Ultrason Ferroelectr Freq Control 2004;51:396–409.
20. De Zordo T, Lill SR, Fink C, Feuchtner GM, Jaschke W, BellmannWeiler R, et al. Real-time sonoelastography of lateral epicondylitis: comparison of findings between patients and healthy volunteers. AJR Am J Roentgenol 2009;193:180–185.
21. Ganne-Carrie N, Ziol M, de Ledinghen V, Douvin C, Marcellin P, Castera L, et al. Accuracy of liver stiffness measurement for the diagnosis of cirrhosis in patients with chronic liver diseases. Hepatology 2006;44:1511–1517.
22. Royer D, Dieulesaint E. Elastic waves in solids I: free and guided propagation. New York: Springer Verlag, 2000.
23. Jeong WK, Lim HK, Lee HK, Jo JM, Kim Y. Principles and clinical application of ultrasound elastography for diffuse liver disease. Ultrasonography 2014;33:149–160.
24. Wu CH, Chen WS, Park GY, Wang TG, Lew HL. Musculoskeletal sonoelastography: a focused review of its diagnostic applications for evaluating tendons and fascia. J Med Ultrasound 2012;20:79–86.
25. Arda K, Ciledag N, Aktas E, Aribas BK, Kose K. Quantitative assessment of normal soft-tissue elasticity using shear-wave ultrasound elastography. AJR Am J Roentgenol 2011;197:532–536.
26. Maisetti O, Hug F, Bouillard K, Nordez A. Characterization of passive elastic properties of the human medial gastrocnemius muscle belly using supersonic shear imaging. J Biomech 2012;45:978–984.
27. Akagi R, Takahashi H. Acute effect of static stretching on hardness of the gastrocnemius muscle. Med Sci Sports Exerc 2013;45:1348–1354.
28. Akagi R, Takahashi H. Effect of a 5-week static stretching program on hardness of the gastrocnemius muscle. Scand J Med Sci Sports 2014;24:950–957.
29. Botanlioglu H, Kantarci F, Kaynak G, Unal Y, Ertan S, Aydingoz O, et al. Shear wave elastography properties of vastus lateralis and vastus medialis obliquus muscles in normal subjects and female patients with patellofemoral pain syndrome. Skeletal Radiol 2013;42:659–666.
30. Umegaki H, Ikezoe T, Nakamura M, Nishishita S, Kobayashi T, Fujita K, et al. Acute effects of static stretching on the hamstrings using shear elastic modulus determined by ultrasound shear wave elastography: differences in flexibility between hamstring muscle components. Man Ther 2015;20:610–613.
31. Shinohara M, Sabra K, Gennisson JL, Fink M, Tanter M. Realtime visualization of muscle stiffness distribution with ultrasound shear wave imaging during muscle contraction. Muscle Nerve 2010;42:438–441.
32. Bouillard K, Nordez A, Hug F. Estimation of individual muscle force using elastography. PLoS One 2011;6:e29261.
33. Yoshitake Y, Takai Y, Kanehisa H, Shinohara M. Muscle shear modulus measured with ultrasound shear-wave elastography across a wide range of contraction intensity. Muscle Nerve 2014;50:103–113.
34. Ates F, Hug F, Bouillard K, Jubeau M, Frappart T, Couade M, et al. Muscle shear elastic modulus is linearly related to muscle torque over the entire range of isometric contraction intensity. J Electromyogr Kinesiol 2015;25:703–708.
35. Bouillard K, Jubeau M, Nordez A, Hug F. Effect of vastus lateralis fatigue on load sharing between quadriceps femoris muscles during isometric knee extensions. J Neurophysiol 2014;111:768–776.
36. Herbert RD, Clarke J, Kwah LK, Diong J, Martin J, Clarke EC, et al. In vivo passive mechanical behaviour of muscle fascicles and tendons in human gastrocnemius muscle-tendon units. J Physiol 2011;589(Pt 21):5257–5267.
37. Aubry S, Risson JR, Kastler A, Barbier-Brion B, Siliman G, Runge M, et al. Biomechanical properties of the calcaneal tendon in vivo assessed by transient shear wave elastography. Skeletal Radiol 2013;42:1143–1150.
38. Hug F, Lacourpaille L, Maisetti O, Nordez A. Slack length of gastrocnemius medialis and Achilles tendon occurs at different ankle angles. J Biomech 2013;46:2534–2538.
39. Lacourpaille L, Hug F, Nordez A. Influence of passive muscle tension on electromechanical delay in humans. PLoS One 2013;8:e53159.
40. Koo TK, Guo JY, Cohen JH, Parker KJ. Quantifying the passive stretching response of human tibialis anterior muscle using shear wave elastography. Clin Biomech (Bristol, Avon) 2014;29:33–39.
41. Chino K, Takahashi H. The association of muscle and tendon elasticity with passive joint stiffness: in vivo measurements using ultrasound shear wave elastography. Clin Biomech (Bristol, Avon) 2015;30:1230–1235.
42. Le Sant G, Ates F, Brasseur JL, Nordez A. Elastography study of hamstring behaviors during passive stretching. PLoS One 2015;10:e0139272.
43. Umehara J, Ikezoe T, Nishishita S, Nakamura M, Umegaki H, Kobayashi T, et al. Effect of hip and knee position on tensor fasciae latae elongation during stretching: an ultrasonic shear wave elastography study. Clin Biomech (Bristol, Avon) 2015;30:1056–1059.
44. Dubois G, Kheireddine W, Vergari C, Bonneau D, Thoreux P, Rouch P, et al. Reliable protocol for shear wave elastography of lower limb muscles at rest and during passive stretching. Ultrasound Med Biol 2015;41:2284–2291.
45. Taniguchi K, Shinohara M, Nozaki S, Katayose M. Acute decrease in the stiffness of resting muscle belly due to static stretching. Scand J Med Sci Sports 2015;25:32–40.
46. Crommert EM, Lacourpaille L, Heales LJ, Tucker K, Hug F. Massage induces an immediate, albeit short-term, reduction in muscle stiffness. Scand J Med Sci Sports 2015;25:e490–e496.
47. Maher RM, Hayes DM, Shinohara M. Quantification of dry needling and posture effects on myofascial trigger points using ultrasound shear-wave elastography. Arch Phys Med Rehabil 2013;94:2146–2150.
48. Aubry S, Nueffer JP, Tanter M, Becce F, Vidal C, Michel F. Viscoelasticity in Achilles tendonopathy: quantitative assessment by using real-time shear-wave elastography. Radiology 2015;274:821–829.
49. Lee SS, Spear S, Rymer WZ. Quantifying changes in material properties of stroke-impaired muscle. Clin Biomech (Bristol, Avon) 2015;30:269–275.
50. Lacourpaille L, Nordez A, Hug F, Couturier A, Dibie C, Guilhem G. Time-course effect of exercise-induced muscle damage on localized muscle mechanical properties assessed using elastography. Acta Physiol (Oxf) 2014;211:135–146.
51. Kot BC, Zhang ZJ, Lee AW, Leung VY, Fu SN. Elastic modulus of muscle and tendon with shear wave ultrasound elastography: variations with different technical settings. PLoS One 2012;7:e44348.
52. Gennisson JL, Deffieux T, Mace E, Montaldo G, Fink M, Tanter M. Viscoelastic and anisotropic mechanical properties of in vivo muscle tissue assessed by supersonic shear imaging. Ultrasound Med Biol 2010;36:789–801.
53. Brum J, Bernal M, Gennisson JL, Tanter M. In vivo evaluation of the elastic anisotropy of the human Achilles tendon using shear wave dispersion analysis. Phys Med Biol 2014;59:505–523.
Supersonic shear wave imaging elastography in pushing mode and imaging mode.A. In pushing mode, four pushes are focused at different depths, and generate spherical shear waves. The constructive interference of the waves creates a quasiplane wave front, which propagates in the opposite direction. B. In imaging mode, the ultrafast acquisition of a wave propagation movie occurs. ARF, acoustic radiation force.
 Fig. 1.Gastrocnemius lateralis muscle of a 27-year-old healthy male.The region of interest is placed in the center of the image and displays qualitative information (color map). The Q - box (circle) enablesthe quantitative measure of Young’s modulus (mean ± standard deviation): 11.0±0.6 kPa, as per a scale that varies from 0 to 180 kPa (top right). This image was acquired using the Aixplorer equipment (source: Laboratory of Biomechanics/PEB/COPPE/UFRJ).
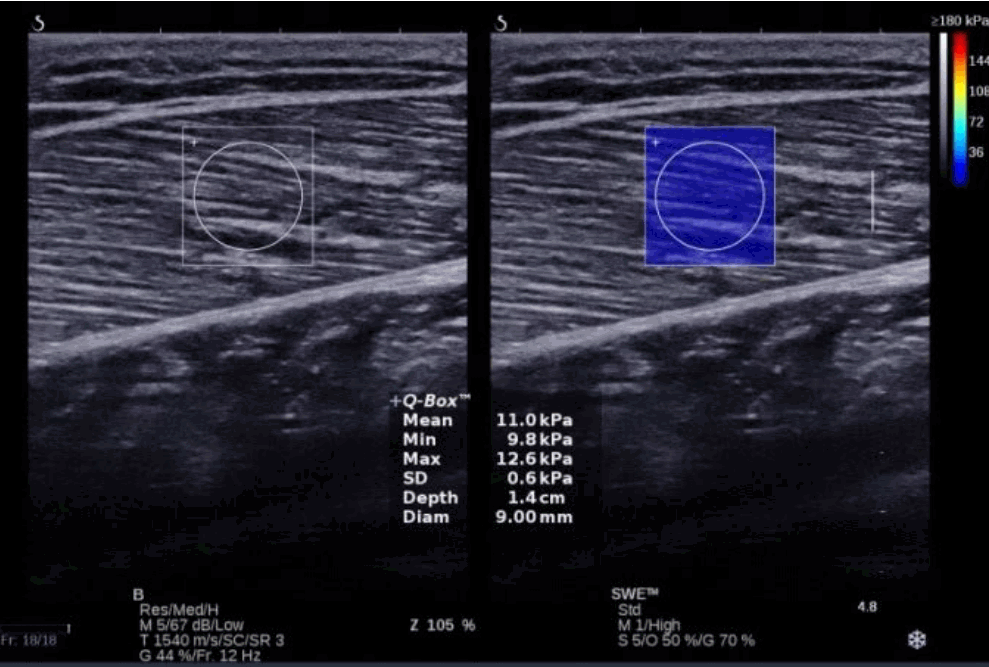 Fig. 2.Elastography images and the spatial average (±standard deviation) values for the Young’s modulus in the selected circular area (α or β).The Young’s modulus in the tibialis anterior (A) and gastrocnemius medialis (C) muscles at rest was relatively homogeneous and smaller than in contraction (B and D, respectively). During contraction with the knee extended (D), the increase in the Young’s modulus was more prominent in the gastrocnemius medialis than the soleus (deeper muscle). In the knee-flexed position, contraction of the plantar flexors (E) increased the Young’s modulus in the gastrocnemius medialis less than in the soleus. During quiet standing (F), there was a greater increase in the Young’s modulus for the gastrocnemius medialis than for the soleus. Reprinted from Shinohara et al. Muscle Nerve 2010;42:438-441 [31], with permission of John Wiley and Sons.
 Fig. 3.Typical example of the shear modulus-lengthening curve for the biceps femoris during passive knee extension at 110° of hip flexion.A notable increase in the shear modulus was observed when the knee was extended (knee angle increase). Reprinted from Le Sant et al. PLoS One 2015;10:e0139272 [42], according to the Creative Commons license.
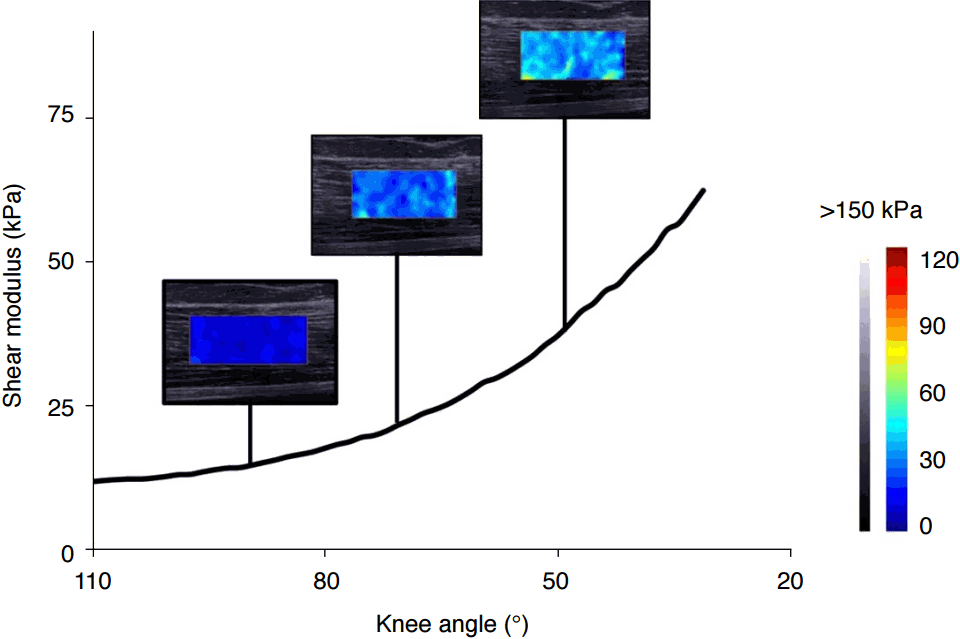 Fig. 4.Typical example of gastrocnemius medialis shear modulus maps obtained at baseline, follow-up 1 (immediately after massage), and follow-up 2 (following 3 minutes of rest).The gastrocnemius medialis shear elastic modulus of the massaged leg was significantly lower immediately after massage (followup 1, 10.3±2.6 kPa) compared with both baseline (11.0±3.1 kPa, P=0.019) and following rest (follow-up 2: 10.9±2.8 kPa; P=0.031). Reprinted from Crommert et al. Scand J Med Sci Sports 2015;25:e490-e496 [46], with permission of John Wiley and Sons.
 Fig. 5.Achilles tendonopathy shear modulus maps.For position 1 (maximal plantar flexion), mean velocity was measured at 3.31 m/sec (A) and at 5.86 m/sec (B) on axial and sagittal images, respectively. For position 2 (neutral position), mean velocity was measured at 4.14 m/sec (C) and at 15.43 m/sec (D), on axial and sagittal images, respectively. N°, number. Reprinted from Aubry et al. Radiology 2015;274:821-829 [48], with permission of Radiological Society of North America.
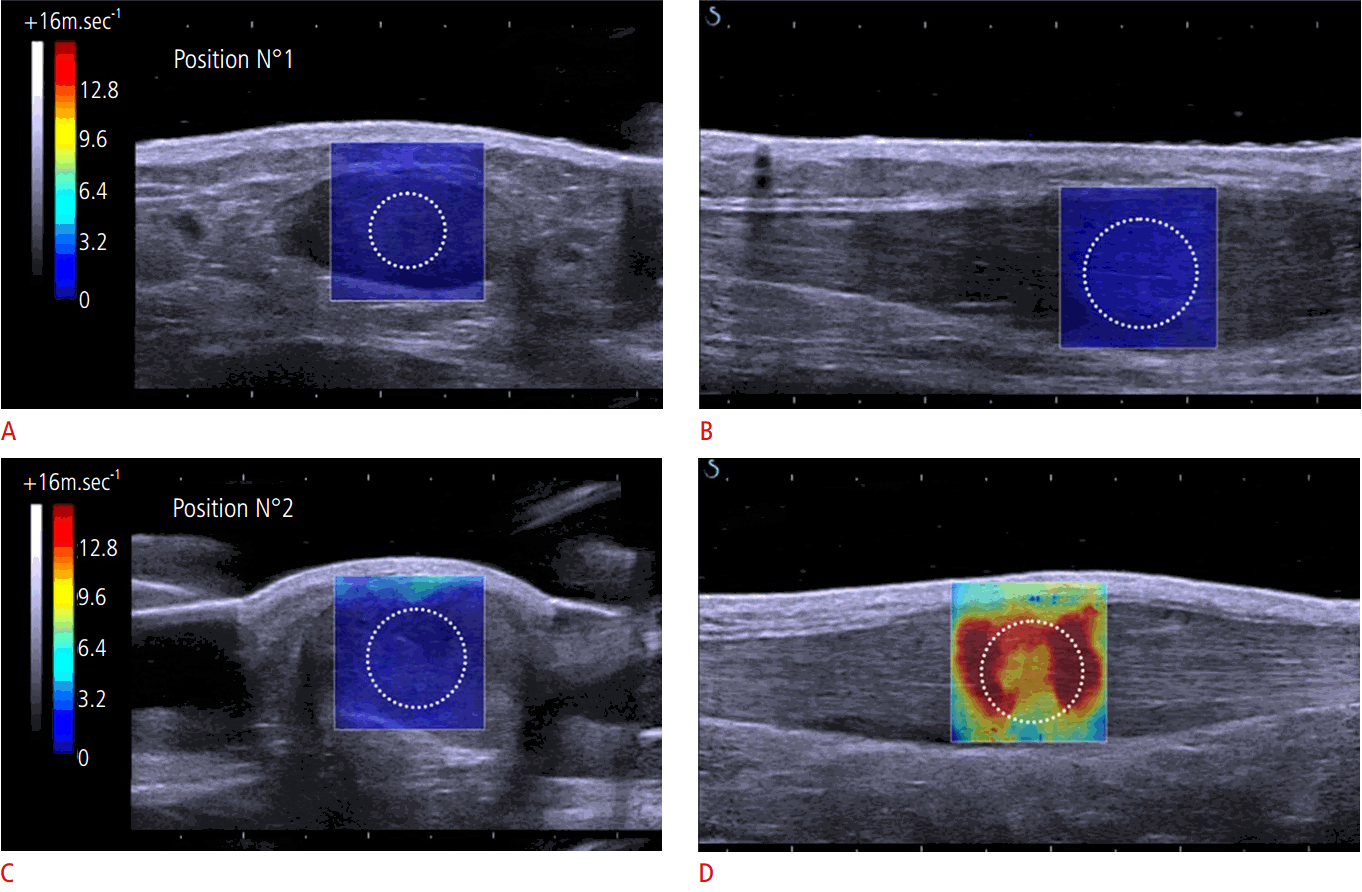 Fig. 6.Biceps brachii muscle shear modulus maps obtained before exercise (PRE), and at 1 hour (1H), 48 hours (48H), and 21 days (21D) post-exercise at an elbow angle of 110°.A significant increase in shear elastic modulus was found at 1 hour, which corresponded to the onset of delayed onset muscle soreness. After 48 hours and 21 days, the shear elastic modulus returned to baseline values. Reprinted and adapted from Lacourpaille et al. Acta Physiol (Oxf) 2014;211:135-146 [50], with permission of John Wiley and Sons.
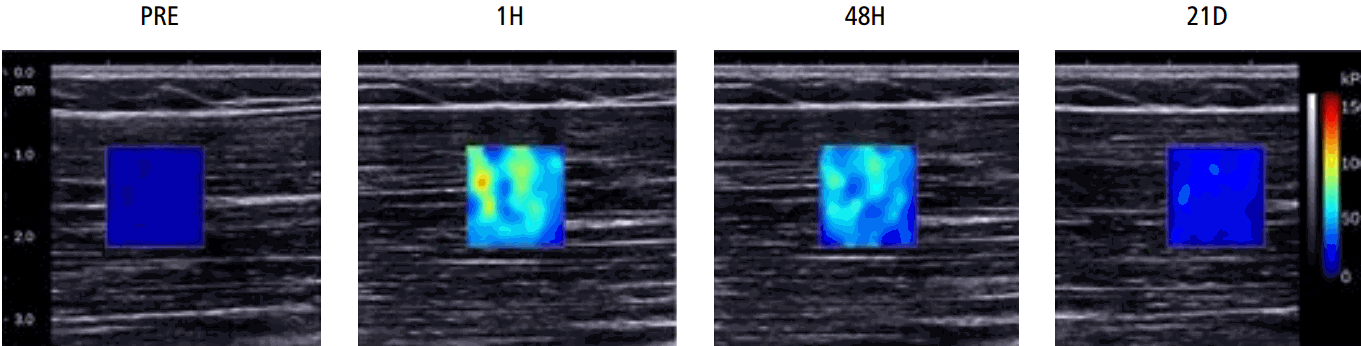 Fig. 7.Rectus femoris muscle shear modulus maps obtained with different transducer pressures. The circle (Q-Box) in the region of interest generates the quantitative information. The pressure of the transducer changed gradually from light to hard. The transducer was kept motionless for 8 to 12 seconds during the acquisition. Reprinted from Kot et al. PLoS One 2012;7:e44348 [51], according to the Creative Commons license.
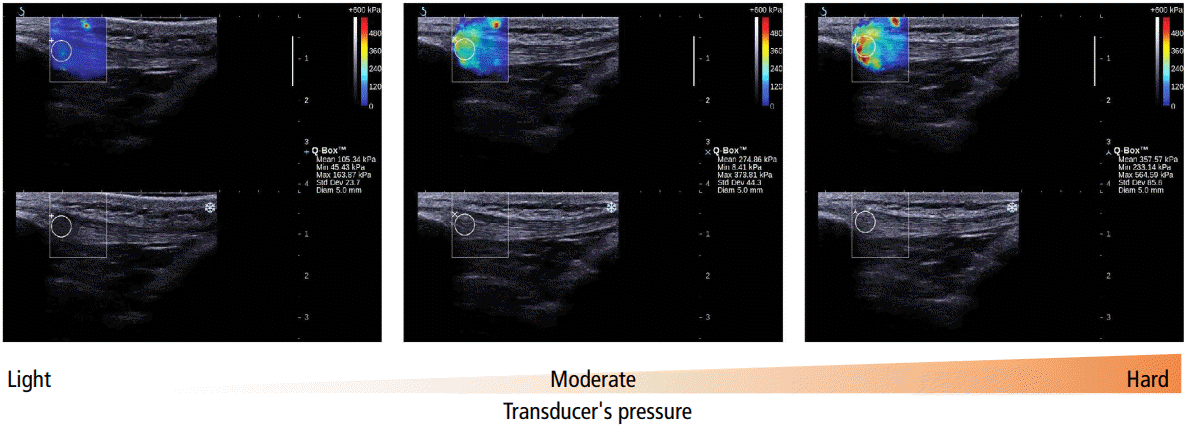 Fig. 8.Table 1.Definitions of mechanical and acoustic parameters Table 2.US elastography methods for human tissue (in vivo) including estimated parameter and main advantages and limitations |



 Print
Print facebook
facebook twitter
twitter Linkedin
Linkedin google+
google+
 Download Citation
Download Citation PDF Links
PDF Links PubReader
PubReader ePub Link
ePub Link Full text via DOI
Full text via DOI Full text via PMC
Full text via PMC




